Consider a directed graph ![]() with n vertices,
with n vertices,
![]() .
The simplest graph representation scheme
uses an
.
The simplest graph representation scheme
uses an ![]() matrix A of zeroes and ones given by
matrix A of zeroes and ones given by
![]()
That is, the ![]() element of the matrix,
is a one only if
element of the matrix,
is a one only if ![]() is an edge in G.
The matrix A is called an
adjacency matrix .
is an edge in G.
The matrix A is called an
adjacency matrix .
For example, the adjacency matrix for graph ![]() in Figure
in Figure ![]() is
is

Clearly, the number of ones in the adjacency matrix is equal to the number of edges in the graph.
One advantage of using an adjacency matrix is that it is easy to
determine the sets of edges emanating from a given vertex.
For example, consider vertex ![]() .
Each one in the
.
Each one in the ![]() row corresponds to an edge
that emanates from vertex
row corresponds to an edge
that emanates from vertex ![]() .
Conversely, each one in the
.
Conversely, each one in the ![]() column
corresponds to an edge incident on vertex
column
corresponds to an edge incident on vertex ![]() .
.
We can also use adjacency matrices to represent undirected graphs.
That is, we represent an undirected graph ![]() with n vertices,
using an
with n vertices,
using an ![]() matrix A of zeroes and ones given by
matrix A of zeroes and ones given by
![]()
Since the two sets ![]() and
and ![]() are equivalent,
matrix A is symmetric about the diagonal.
That is,
are equivalent,
matrix A is symmetric about the diagonal.
That is, ![]() .
Furthermore, all of the entries on the diagonal are zero.
That is,
.
Furthermore, all of the entries on the diagonal are zero.
That is, ![]() for
for ![]() .
.
For example, the adjacency matrix for graph ![]() in Figure
in Figure ![]() is
is
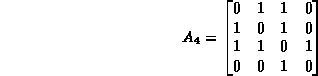
In this case, there are twice as many ones in the adjacency matrix as there are edges in the undirected graph.
A simple variation allows us to use an adjacency matrix
to represent an edge-labeled graph.
For example, given numeric edge labels,
we can represent a graph (directed or undirected)
using an ![]() matrix A in which the
matrix A in which the ![]() is the numeric label associated with edge
is the numeric label associated with edge ![]() in the case of a directed graph,
and edge
in the case of a directed graph,
and edge ![]() ,
in an undirected graph.
,
in an undirected graph.
For example, the adjacency matrix for the graph ![]() in Figure
in Figure ![]() is
is
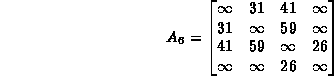
In this case, the array entries corresponding to non-existent edges
have all been set to ![]() .
Here
.
Here ![]() serves as a kind of sentinel .
The value to use for the sentinel depends on the application.
For example, if the edges represent routes between geographic locations,
then a route of length
serves as a kind of sentinel .
The value to use for the sentinel depends on the application.
For example, if the edges represent routes between geographic locations,
then a route of length ![]() is much like one that does not exist.
is much like one that does not exist.
Since the adjacency matrix has ![]() entries,
the amount of spaced needed to represent the edges of
a graph is
entries,
the amount of spaced needed to represent the edges of
a graph is ![]() ,
regardless of the actual number of edges in the graph.
If the graph contains relatively few edges,
e.g., if
,
regardless of the actual number of edges in the graph.
If the graph contains relatively few edges,
e.g., if ![]() ,
then most of the elements of the adjacency matrix will be zero (or
,
then most of the elements of the adjacency matrix will be zero (or ![]() ).
A matrix in which most of the elements are zero (or
).
A matrix in which most of the elements are zero (or ![]() )
is a sparse matrix .
)
is a sparse matrix .