4.3 Performance Analysis

  When composing components to form programs, we also need to consider   how to compose their performance models. For example, consider a program that combines two components a and b with performance models as follows:

In the case of a sequential composition of a and b that does not require data redistribution, a performance model for the resulting program may sometimes be obtained simply by summing the components of 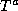and :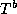

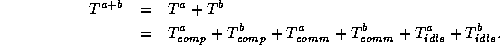
In practice, the performance analysis of programs constructed from multiple modules is often complicated by the following factors. Fortunately, these complications can be accounted for by using the modeling techniques of Chapter 3.

Increased computation. Data transfer between modules can require computation, thereby increasing total computation costs. Less frequently, the merging of two modules will allow us to reduce computation costs by eliminating operations that are common to both components.

Reduced idle time. Recall that idle time represents time spent doing no useful work, either because a processor has completed its part of a computation early or because the processor is waiting for   data. Idle time can be reduced in concurrent compositions if computation or communication in one module can proceed when other modules mapped to the same processors are idle.

Increased communication. Composition often introduces a need for additional communication. In sequential composition, communication may be required to redistribute data structures at component boundaries. In parallel composition, communication is required to move data between modules executing on different processors.

  Increased granularity. Parallel composition tends to increase computation and communication granularity within composed components, because each executes within a subset of available processors. This effect can improve overall performance.

Load imbalances. Parallel composition can increase idle time   if the computational resources allocated to different components do not allow the components to execute at equal rates. In this situation, one module will complete some phase of a computation before another and must then remain idle until the other module provides the data required to continue execution. This is a variant of the load-balancing problem discussed in Chapter 2.