Differentiation Theorem

Let $x(t)$ denote a function differentiable for all $t$ such that $x(\pm\infty)=0$ and the Fourier Transforms (FT) of both $x(t)$ and $x^\prime(t)$ exist, where $x^\prime(t)$ denotes the time derivative of $x(t)$. Then we have

$$\zbox {x^\prime(t) \;\longleftrightarrow\;j\omega X(\omega)}$$

where $X(\omega)$ denotes the Fourier transform of $x(t)$. In operator notation:

$$\zbox {\hbox{\sc FT}_{\omega}(x^\prime) = j\omega X(\omega)}$$

Proof: This follows immediately from integration by parts:

$$\begin{eqnarray*} \hbox{\sc FT}_{\omega}(x^\prime) &\isdef & \int_{-\infty}^\in... ...\infty x(t) (-j\omega)e^{-j\omega t} dt\\ &=& j\omega X(\omega) \end{eqnarray*}$$

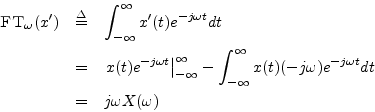
since $x(\pm\infty)=0$.

The differentiation theorem is implicitly used in §E.6 to show that audio signals are perceptually equivalent to bandlimited signals which are infinitely differentiable for all time.