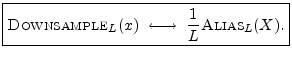
Theorem: For all
Theorem: For all
![]() ,
,
Proof: Let
![]() denote the frequency index in the
aliased spectrum, and
let
denote the frequency index in the
aliased spectrum, and
let
![]() . Then
. Then ![]() is length
is length ![]() ,
where
,
where ![]() is the downsampling factor. We have
is the downsampling factor. We have
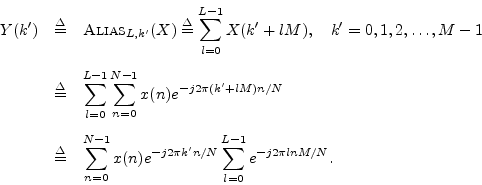
Since ![]() , the sum over
, the sum over ![]() becomes
becomes
![$\displaystyle \sum_{l=0}^{L-1}\left[e^{-j2\pi n/L}\right]^l =
\frac{1-e^{-j2\p...
...right) \\ [5pt]
0, & n\neq 0 \left(\mbox{mod}\;L\right) \\
\end{array}\right.
$](img1417.png)
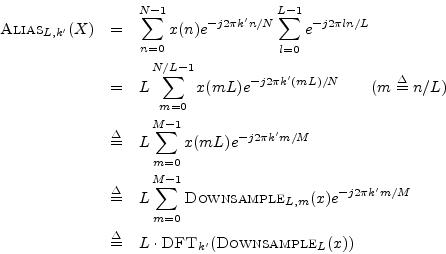
Since the above derivation also works in reverse, the theorem is proved.
An illustration of aliasing in the frequency domain is shown in Fig.7.12.