Let
![]() denote the
denote the ![]() th sample of the original
sound
th sample of the original
sound ![]() , where
, where ![]() is time in seconds. Thus,
is time in seconds. Thus, ![]() ranges over the
integers, and
ranges over the
integers, and ![]() is the sampling interval in seconds. The
sampling rate in Hertz (Hz) is just the reciprocal of the
sampling period,
i.e.,
is the sampling interval in seconds. The
sampling rate in Hertz (Hz) is just the reciprocal of the
sampling period,
i.e.,
To avoid losing any information as a result of sampling, we must
assume ![]() is bandlimited to less than half the sampling
rate. This means there can be no energy in
is bandlimited to less than half the sampling
rate. This means there can be no energy in ![]() at frequency
at frequency
![]() or above. We will prove this mathematically when we prove
the sampling theorem in §D.3 below.
or above. We will prove this mathematically when we prove
the sampling theorem in §D.3 below.
Let ![]() denote the Fourier transform of
denote the Fourier transform of ![]() , i.e.,
, i.e.,
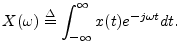
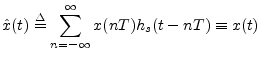
The reconstruction of a sound from its samples can thus be interpreted as follows: convert the sample stream into a weighted impulse train, and pass that signal through an ideal lowpass filter which cuts off at half the sampling rate. These are the fundamental steps of digital to analog conversion (DAC). In practice, neither the impulses nor the lowpass filter are ideal, but they are usually close enough to ideal that one cannot hear any difference. Practical lowpass-filter design is discussed in the context of bandlimited interpolation [70].