e^(j theta)

We've now defined $a^z$ for any positive real number $a$ and any complex number $z$. Setting $a=e$ and $z=j\theta$ gives us the special case we need for Euler's identity. Since $e^x$ is its own derivative, the Taylor series expansion for $f(x)=e^x$ is one of the simplest imaginable infinite series:

$$e^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \cdots$$

The simplicity comes about because $f^{(n)}(0)=1$ for all $n$ and because we chose to expand about the point $x=0$. We of course define

$$e^{j\theta} \isdef \sum_{n=0}^\infty \frac{(j\theta)^n}{n!} = 1 + j\theta - \frac{\theta^2}{2} - j\frac{\theta^3}{3!} + \cdots \,.$$

Note that all even order terms are real while all odd order terms are imaginary. Separating out the real and imaginary parts gives

$$\begin{eqnarray*} \mbox{re}\left\{e^{j\theta}\right\} &=& 1 - \theta^2/2 + \thet... ...heta}\right\} &=& \theta - \theta^3/3! + \theta^5/5! - \cdots\,. \end{eqnarray*}$$

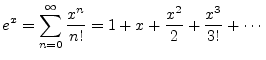
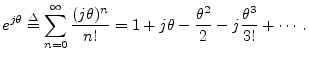
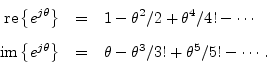
Comparing the Maclaurin expansion for $e^{j\theta }$ with that of $\cos(\theta)$ and $\sin(\theta)$ proves Euler's identity. Recall from introductory calculus that

$$\begin{eqnarray*} \frac{d}{d\theta}\cos(\theta) &=& -\sin(\theta) \\ [5pt] \frac{d}{d\theta}\sin(\theta) &=& \cos(\theta) \end{eqnarray*}$$

so that

$$\begin{eqnarray*} \left.\frac{d^n}{d\theta^n}\cos(\theta)\right\vert _{\theta=0}... ...} \\ [5pt] 0, & n\;\mbox{\small even}. \\ \end{array} \right. \end{eqnarray*}$$

Plugging into the general Maclaurin series gives

$$\begin{eqnarray*} \cos(\theta) &=& \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}\theta... ...mbox{\tiny$n$\ odd}}}^\infty \frac{(-1)^{(n-1)/2}}{n!} \theta^n. \end{eqnarray*}$$

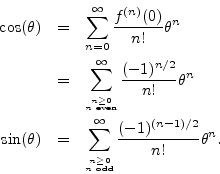
Separating the Maclaurin expansion for $e^{j\theta }$ into its even and odd terms (real and imaginary parts) gives

$$\begin{eqnarray*} e^{j\theta} \isdef \sum_{n=0}^\infty \frac{(j\theta)^n}{n!} &... ...-1)^{(n-1)/2}}{n!} \theta^n\\ &=& \cos(\theta) + j\sin(\theta) \end{eqnarray*}$$

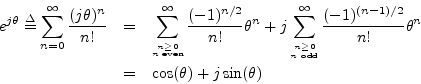
thus proving Euler's identity.