Group Constructors

  Group constructors are used to construct new groups from existing groups, using various set operations. These are local operations, and distinct groups may be defined on different processes; a process may also define a group that does not include itself. Consistent definitions are required when groups are used as arguments in communicator-building functions. MPI does not provide a mechanism to build a group from scratch, but only from other, previously defined groups. The base group, upon which all other groups are defined, is the group associated with the initial communicator MPI_COMM_WORLD (accessible through the function MPI_COMM_GROUP).

Local group creation functions are useful since some applications have the needed information distributed on all nodes. Thus, new groups can be created locally without communication. This can significantly reduce the necessary communication in creating a new communicator to use this group.

In Section , communicator creation functions are described which also create new groups. These are more general group creation functions where the information does not have to be local to each node. They are part of communicator creation since they will normally require communication for group creation. Since communicator creation may also require communication, it is logical to group these two functions together for this case.

MPI_Comm_group(MPI_Comm comm, MPI_Group *group)

MPI_COMM_GROUP(COMM, GROUP, IERROR)INTEGER COMM, GROUP, IERROR

MPI_COMM_GROUP returns in group a handle to the group of comm.

The following three functions do standard set type operations. The only difference is that ordering is important so that ranks are consistently defined.

  MPI_GROUP_UNION(group1, group2, newgroup)

     IN      group1          first group
     IN      group2          second group2
     OUT     newgroup        union group

MPI_Group_union(MPI_Group group1, MPI_Group group2, MPI_Group *newgroup)

MPI_GROUP_UNION(GROUP1, GROUP2, NEWGROUP, IERROR)INTEGER GROUP1, GROUP2, NEWGROUP, IERROR

  MPI_GROUP_INTERSECTION(group1, group2, newgroup)

     IN      group1          first group
     IN      group2          second group2
     OUT     newgroup        intersection group

MPI_Group_intersection(MPI_Group group1, MPI_Group group2, MPI_Group *newgroup)

MPI_GROUP_INTERSECTION(GROUP1, GROUP2, NEWGROUP, IERROR)INTEGER GROUP1, GROUP2, NEWGROUP, IERROR

  MPI_GROUP_DIFFERENCE(group1, group2, newgroup)

     IN      group1          first group
     IN      group2          second group2
     OUT     newgroup        difference group

MPI_Group_difference(MPI_Group group1, MPI_Group group2, MPI_Group *newgroup)

MPI_GROUP_DIFFERENCE(GROUP1, GROUP2, NEWGROUP, IERROR)INTEGER GROUP1, GROUP2, NEWGROUP, IERROR

The operations are defined as follows:

union

All elements of the first group (group1), followed by all elements of second group (group2) not in first.

intersection

All elements of the first group that are also in the second group, ordered as in first group.

difference

All elements of the first group that are not in the second group, ordered as in the first group.

The new group can be empty, that is, equal to MPI_GROUP_EMPTY. MPI_GROUP_EMPTY

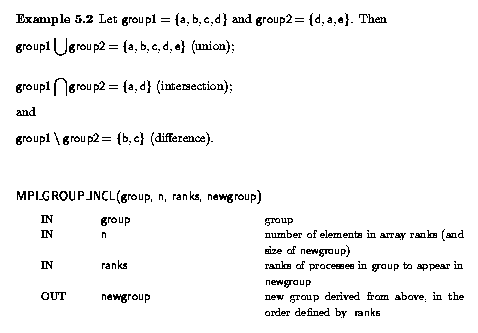
MPI_Group_incl(MPI_Group group, int n, int *ranks, MPI_Group *newgroup)

MPI_GROUP_INCL(GROUP, N, RANKS, NEWGROUP, IERROR)INTEGER GROUP, N, RANKS(*), NEWGROUP, IERROR

The function MPI_GROUP_INCL creates a group newgroup that consists of the n processes in group with ranks rank[0],..., rank[n-1]; the process with rank i in newgroup is the process with rank ranks[i] in group. Each of the n elements of ranks must be a valid rank in group and all elements must be distinct, or else the call is erroneous. If n = 0, then newgroup is MPI_GROUP_EMPTY. MPI_GROUP_EMPTY This function can, for instance, be used to reorder the elements of a group.

MPI_Group_excl(MPI_Group group, int n, int *ranks, MPI_Group *newgroup)

MPI_GROUP_EXCL(GROUP, N, RANKS, NEWGROUP, IERROR)INTEGER GROUP, N, RANKS(*), NEWGROUP, IERROR

The function MPI_GROUP_EXCL creates a group of processes newgroup that is obtained by deleting from group those processes with ranks ranks[0],..., ranks[n-1] in C or ranks[1],..., ranks[n] in Fortran. The ordering of processes in newgroup is identical to the ordering in group. Each of the n elements of ranks must be a valid rank in group and all elements must be distinct; otherwise, the call is erroneous. If n = 0, then newgroup is identical to group.

Example5.4 Let group be a handle to the group {a, b, c, d, e, f}
    and let ranks = (3, 1, 2) Then a handle to the group {a, e, f}
    is returned in newgroup.

MPI_Group_range_incl(MPI_Group group, int n, int ranges[][3], MPI_Group *newgroup)

MPI_GROUP_RANGE_INCL(GROUP, N, RANGES, NEWGROUP, IERROR)INTEGER GROUP, N, RANGES(3,*), NEWGROUP, IERROR

Each triplet in ranges specifies a sequence of ranks for processes to be included in the newly created group. The newly created group contains the processes specified by the first triplet, followed by the processes specified by the second triplet, etc.

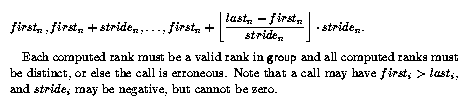
The functionality of this routine is specified to be equivalent to expanding the array of ranges to an array of the included ranks and passing the resulting array of ranks and other arguments to MPI_GROUP_INCL. A call to MPI_GROUP_INCL is equivalent to a call to MPI_GROUP_RANGE_INCL with each rank i in ranks replaced by the triplet (i,i,1) in the argument ranges.

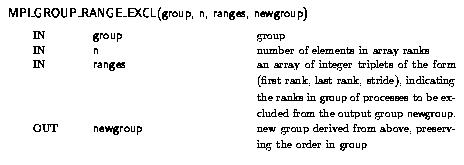
MPI_Group_range_excl(MPI_Group group, int n, int ranges[][3], MPI_Group *newgroup)

MPI_GROUP_RANGE_EXCL(GROUP, N, RANGES, NEWGROUP, IERROR)INTEGER GROUP, N, RANGES(3,*), NEWGROUP, IERROR

Each triplet in ranges specifies a sequence of ranks for processes to be excluded from the newly created group. The newly created group contains the remaining processes, ordered as in group.

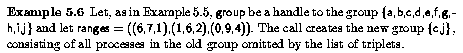
Each computed rank must be a valid rank in group and all computed ranks must be distinct, or else the call is erroneous.

The functionality of this routine is specified to be equivalent to expanding the array of ranges to an array of the excluded ranks and passing the resulting array of ranks and other arguments to MPI_GROUP_EXCL. A call to MPI_GROUP_EXCL is equivalent to a call to MPI_GROUP_RANGE_EXCL with each rank i in ranks replaced by the triplet (i,i,1) in the argument ranges.