CSCI 2150
Spring 2002 Test 2 -- Answers

The following is the set of answers to the Spring 2002 CSCI 2150 Test 2. In some cases, where the HTML does not prohibit it, I've elaborated on the process to get to the answers.

1. Fill out the truth table to the right for all possible combinations of inputs for the circuit below. (Circuit not shown in answer sheet.)
   
   Answer:
   

   Inputs		Outputs
   ^S	^R	Q	^Q
   0	0	illegal
   0	1	1	0
   1	0	0	1
   1	1	Q0	^Q0

   
   
2. In a truth table, the symbol (arrow pointing upward) indicates that the input is:
   
   Answer: d) changing from a 0 to a 1 (rising edge).
   
   
3. Show the D flip-flop output waveform Q based on the inputs D and CLK indicated in the figure below. Assume the flip-flop captures on the rising edge.
   
   Answer:
   
   
   
   
4. Create the next state truth table and the output truth table for the state diagram below. (The diagram is omitted from this answer key. You can see it from the PDF file of the test.) Use the variable names S1 and S0 to represent the most significant and least significant bits respectively of the binary number identifying the state.
   
   Answer:
   
   

   Current State		Input P	Next State
   S1	S0		S1'	S0'
   0	0	0	0	0
   0	0	1	1	0
   0	1	0	1	1
   0	1	1	1	0
   1	0	0	1	1
   1	0	1	1	0
   1	1	0	0	0
   1	1	1	0	1

   
   
   
5. Which of the following circuits can be used to divide the frequency of the input F by 2?
   
   Answer:
   
   
   
   
6. Assuming the state the machine always begins in "init", identify the error in this state diagram? Be as specific as you can.
   
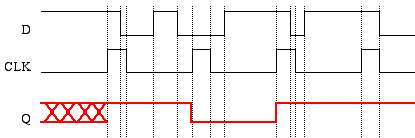
   Answer:
   
   It is impossible to get to state "three". Since it is impossible to get to the state, it has no place in the state diagram.
   
   
7. What is the minimum number of flip-flops it would take to realize a state machine with 42 states?
   
   Answer:
   
   First, you must understand that 42 states must be represented with 42 different binary values, i.e., the binary equivalents of 0 through 41. Once you know this, there are a couple of ways to do this. You can convert 41 to binary and get 101001₂. After you get rid of any leading zeros, you should see that this number requires 6 binary digits. Therefore, it takes 6 flip-flops to represent the states of a state machine with 42 states.
   
   The second way to do this is to look at the powers of two and find where 42 falls.
   
   

   21	2
   22	4
   23	8
   24	16
   25	32
   26	64
   27	128

   
   Since 42 lies between 32 and 64, then the number of flip-flops required equals the power that 2 is raised to for the upper limit of 64. Once again, this is 6.
   
   
8. The three Boolean expressions below represent the next state bits (S0' and S1') and the output bit (X) based on the current state (S0 and S1). Draw the logic circuit for the state machine including the flip-flops and output circuitry. Be sure to label flip-flop inputs and other signals.
   
   S₀' = S₀ + ^S₁
   S₁' = ^S₁ S₀
   X = ^S₁ S₀ + ^S₀ S₁
   
   Answer:
   
   
   
   
9. For the multiplexer/selector shown to the right, sketch the output waveform Y for the inputs S0 and S1 shown in the graph below. Assume S1 is the most significant bit.
   
   Answer:
   
   
   
   
10. For the active-low output decoder shown to the right, fill in the values for all of the outputs D0 through D7. Assume S2 is most significant bit.
    
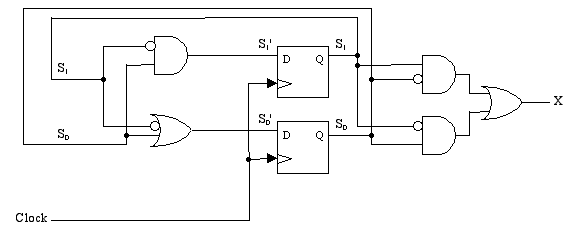
    Answer:
    
    The inputs to the decoder act as a channel selector determining which of the outputs receives the "active low" output. Since the inputs to the decoder (in order of significance) are 101, and since the decimal equivalent of 101 is 5, then output D₅ equals zero. All of the other outputs equal 1.
    
    
11. How many D flip-flops are contained in a 16-bit RAM with 24 address lines? (Don't do the calculation; only write the equation with the correct values.)
    
    Answer: Since there are 24 address lines, then there must be 2²⁴ different addresses or rows. Since there are 16 data bits (columns) per address, then the answer is 2²⁴ * 16.
    
    
12. Why is a cache RAM smaller than a regular RAM?
    
    Answer: To be faster.
    
    
13. Draw a line between the memory type on the left and its most appropriate characteristic on the right.
    
    Answer:
    
    
    
    
14. True or False -- A DRAM is more expensive than an SRAM of the same size.
    
    Answer: False -- The capacitors that make up a DRAM are far cheaper than flip-flops.
    
    
15. True or False -- A DRAM has higher densities than an SRAM.
    
    Answer: True -- The capacitors that make up a DRAM are far smaller than flip-flops and therefore more can be packed into the same space.
    
    
16. What are the high and low addresses of the memory range defined with the chip select shown to the right?
    
    Answer: Examining the circuit reveals that to have the chip select go to zero, the address values must be A₁₅ = 0, A₁₄ = 0, A₁₃ = 1, A₁₂ = 0, and A₁₁ = 1.
    
    

    A15

    A14

    A13

    A12

    A11

    A10

    A9

    A8

    A7

    A6

    A5

    A4

    A3

    A2

    A1

    A0

    0

    0

    1

    0

    1

    X

    X

    X

    X

    X

    X

    X

    X

    X

    X

    X

    
    The low address should have 0's in all of the positions where X's are in the table above and the high address should have 1's. Therefore, the low address should be:
    
    

    A15	A14	A13	A12	A11	A10	A9	A8	A7	A6	A5	A4	A3	A2	A1	A0
    0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	0

    
    Converting to hex we get a low address of 2800₁₆.
    
    The high address should be:
    
    

    A15	A14	A13	A12	A11	A10	A9	A8	A7	A6	A5	A4	A3	A2	A1	A0
    0	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1

    
    Converting to hex we get a high address of 2FFF₁₆.
    
    
17. For the chip select in problem 16, how big is the memory chip that uses the chip select?
    
    Answer: The size of the section of memory reserved by a chip select is determined by the number of bits that are allowed to change from 0 to 1 in the range. In problem 16, bits A₀ through A₁₀ are allowed to change, 11 bits. Therefore, the size of the section of memory reserved by the chip select.
    
    Size of memory = 2¹¹ = 2K
    
    
18. How many 128K memories can be fit into the memory space of a microprocessor with 27 address lines?
    
    Answer: The answer can be found one of two ways. First, you can figure out the size of the processor's memory space (dictated by the 27 address lines), then divide 128K into that.
    
    2²⁷ = 128 Meg
    
    128 Meg/128K = 1024 times
    
    The other way is to figure out how many lines are left for the chip select after taking out the address lines for the 128K memories. Since 128K takes 17 address lines, then 27 - 17 = 10 lines are left. That means we can have 2¹⁰ = 1024 different chip select circuits.
    
    
19. True or false: A single memory space can have a low address of 2500₁₆ and a high address of 27FF₁₆.
    
    Answer: False
    
    First, convert each of these addresses into binary.
    
    

    Address bits:	A15	A14	A13	A12	A11	A10	A9	A8	A7	A6	A5	A4	A3	A2	A1	A0
    Low address:	0	0	1	0	0	1	0	1	0	0	0	0	0	0	0	0
    High address:	0	0	1	0	0	1	1	1	1	1	1	1	1	1	1	1

    
    Can we draw a line where both the high and the low address have EXACTLY the same bits to the left of the line and the low address has all zeros to the right and the high address has all ones?
    
    Well, if we draw the line between bits 10 and 11, then bit 9 doesn't follow the requirement where all the bits of the low address must be 0 to the right of the line. If we draw the line between bits 9 and 8, then all of the bits to the left of the line do not stay the same for the low and the high addresses.
    
    Therefore, since we can't draw this line, there is no way that these addresses can be the high and low limits of a single chip select.
    
    
20. True or false: A 2K memory chip can have a low address of A9800₁₆.
    
    Answer: True
    
    To determine the answer to this problem, we need to begin by figuring out how many bits the 2K memory needs for its own address lines. Since 211 = 2K, then we know that 11 address lines will be needed. Now we need to figure out if the low address above has its 11 least significant bits set to zero. (That allows the address to follow the rules outlined in problem 19.)
    
    

    A19	A18	A17	A16	A15	A14	A13	A12	A11	A10	A9	A8	A7	A6	A5	A4	A3	A2	A1	A0
    1	0	1	0	1	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0

    
    Counting from the right side of this binary value, we count eleven zeros before we encounter our first 1. Therefore, this address can be the low address of a 2K chip select.
    
    
21. Using logic gates, design a chip select for an 8K RAM placed in a 128K memory space with a low address of 6000₁₆. Label all address lines used for chip select.
    
    Answer:
    
    
    

Created by David Tarnoff for use by his sections of CSCI 2150.