


2.1 EXPERIMENT, SAMPLE SPACE, AND EVENTSEach probabilistic situation that we wish to analyze can be viewed in the context of an experiment. By experiment we mean any nondeterministic process that has a number of distinct possible outcomes. Thus, an experiment is first characterized by a list of possible outcomes. A particular performance of the experiment, sometimes referred to as an experimental trial, yields one and only one of the outcomes.
The finest-grained list of outcomes for an experiment is the sample
space of the experiment. Examples of sample spaces are:
Probabilistic analysis requires considerable manipulation in an
experiment's sample space. For this, we require knowledge of the algebra
of events, where an event is defined to be a collection of points in the
sample space. A generic event is given an arbitrary label, such as A, B,
or C. Since the entire sample space defines the universe of our
concerns,
it is called 
Events A1 A2, . . . , AN are said to be collectively exhaustive if they include all points in the universe of events: 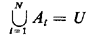
A set of events A1, A2,...,AN that are both mutually exclusive and collectively exhaustive contains each point of the sample space U in one and only one of the events Ai Given these notions, we can more carefully define a sample space as follows: Definition: A sample space is the finest-grained, mutually exclusive, collectively exhaustive listing of all possible outcomes of an experiment. The first (and perhaps most important) step in constructing a probabilistic model consists of identifying the sample space for the corresponding experiment. Example 1: Stick Cutting A simple example drawn from geometrical probability will serve to illustrate some of these ideas. Suppose that two points are marked (in some nondeterministic way) on a stick of length I meter. a. Define the sample space for this experiment. b. Identify the event, "The second point is to the left of the first point." C. Suppose that the stick is cut at the marked points. Identify the event, "A triangle can be formed with the resulting three pieces." Solution: a. Call the first point x1 and the second x2. Since we are given no information about x1 and x2 other than that each is between 0 and 1, the sample space is the collection of points in the unit square shown in Figure 2.1. b. The event indicated, call it E1, corresponds to (x1 > x2). This set of points lies in the triangular region of the sample space below the line x2 = x1. c. Let 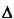 be the event that a triangle can be formed. Identification
of A
in the (x1, x2) sample space requires a bit more care than in the case
of
the event E1 = (x1 > x2). Suppose that, in fact,
x1 > x2. Then the three
stick lengths are x2, x1 - x2, and 1 - x1. For a triangle to be formed,
each length must be less than 1/2: be the event that a triangle can be formed. Identification
of A
in the (x1, x2) sample space requires a bit more care than in the case
of
the event E1 = (x1 > x2). Suppose that, in fact,
x1 > x2. Then the three
stick lengths are x2, x1 - x2, and 1 - x1. For a triangle to be formed,
each length must be less than 1/2: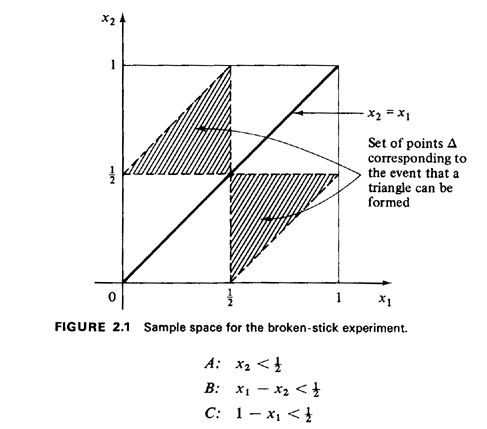
So, given x1 > x2, 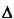 is composed of the set of points that simultaneously satisfies these
three
inequalities or, equivalently, the set of points in
is composed of the set of points that simultaneously satisfies these
three
inequalities or, equivalently, the set of points inThe resulting set is contained in the lower triangle of area 1/8 in the sample space. Now suppose that (X1  X2)=E'1
Here we can invoke symmetry. A current dictionary defines symmetry as
"similarity
of form or arrangement on either side of a dividing
line or plane; correspondence of opposite parts in size, shape, and
position."1 Since the labeling of points x1 and x2 was totally
arbitrary,
there exists symmetry about the line x1 = x2. Thus, we obtain a similar
triangle of area 1/8 above the line x1 = x2. X2)=E'1
Here we can invoke symmetry. A current dictionary defines symmetry as
"similarity
of form or arrangement on either side of a dividing
line or plane; correspondence of opposite parts in size, shape, and
position."1 Since the labeling of points x1 and x2 was totally
arbitrary,
there exists symmetry about the line x1 = x2. Thus, we obtain a similar
triangle of area 1/8 above the line x1 = x2.As one final point, we may wish to express A in terms of the algebra of events. If we define 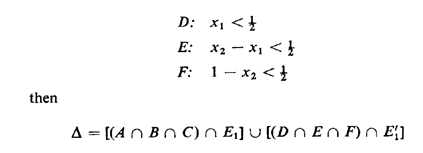
In modeling experiments, extreme care must be given to a precise interpretation of the word statement. Statements that may at first sound the same may actually imply markedly different experiments; or, statements may simply be imprecise and ambiguous. A famous illustration of this in a geometrical setting, known as Bertrand's paradox (1907), yields three different answers to the question: What is the probability that a "random chord" of a circle of unit radius has a length greater than 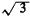 the side of an inscribed equilateral triangle ?2
Each of the three
solutions, which we will develop in Chapter 3, is "correct" since each
involves a different interpretation of that difficult word "random." the side of an inscribed equilateral triangle ?2
Each of the three
solutions, which we will develop in Chapter 3, is "correct" since each
involves a different interpretation of that difficult word "random."To strengthen your understanding of word statements as they relate to concepts of sample space and event, try the following two exercises: Exercise 2.1: Stick Breaking, mod 2 Repeat parts (a) and (c) of the triangle problem described in Example 1, given that the problem statement is changed as follows: "A point is marked (in some random way) on a stick of length 1 meter. Then a second point is marked on the stick (in some random way) to the left of the first point." Exercise 2.2: Stick Breaking, Still Again! Repeat parts (a), (b), and (c) of the triangle problem given that the problem statement is changed as follows: "A point is marked (in some random way) on a stick of length 1 meter. The stick is then cut at that point. Another point is marked (in some random way) on the larger of the two resulting stick pieces." 1 Webster's New World Dictionary of the English Language, Second College Edition, World Publishing Co., New York, 1974, p. 1442. 2 J. Bertrand, Calcul des probabilities, Paris, 1907 |


