


2.9.4 Poisson PMFA random variable K has a Poisson pmf if 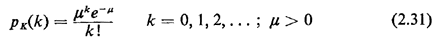
Substituting into the definition of the z-transform, we obtain 
Differentiating (2.32) and substituting in (2.18) and (2.20), the mean and variance are found to be equal: 
In our work the Poisson pmf will arise most frequently in describing Poisson processes. These are processes in which "Poisson-type events" or "arrivals" are distributed totally randomly in time (or in space-see Section 3.4). In urban service systems, the Poisson process can be used as a reasonable model for the process generating fire alarms, police calls, ambulance calls, inquiries at a "little city hall," traffic passing through a lightly traveled intersection, breakdowns in a city's fleet of vehicles, letters arriving on the desk of a city administrator, the filled trash cans produced by a household, traffic violators on a given street segment, and so on. With the (time) Poisson process, we suppose that the process commences at t = 0 and that at random times t1, t2, . . . , Poisson-type events occur (see Figure 2.6). Suppose that 
|


