3.7.3 Expected Travel Distances: The General Case
Our discussion, so far, has focused primarily
on exact and
approximate expressions for expected travel distances and times to
and from incidents in
districts with relatively regular ("fairly compact and fairly
convex")
geometries and uniform distribution of incidents over the districts.
Although this focus
may appear, at first, to cover only a limited subset of the cases
that one may encounter,
it turns out that, in practice, our results can be used as
"building blocks" to
obtain good approximations in a large number of cases where
incidents are not uniformly
distributed and the district itself does not have a nice rectangular
(or circular,
triangular, etc.) shape.
Before illustrating this, let us first discuss,
in the abstract, the
most general possible cases. Let (X, Y) and
(X1,
Y1,) indicate,
respectively, the location of
calls for service and of the response unit in a district R of area
A. Denote by fx,y,x1,y1
(x,y,x1,y1) the joint pdf for random
variables X, Y, X1,
and Y1, and by D =
d[(X1,
Y1,), (X, Y)] the
mathematical relationship for
the distance between (X1,
Y1,)
and (X, Y) [e.g., D = 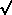 [(X1
- X)2 + (Y1
- Y)2]
for Euclidean distances]. Then, for the expected travel distance in
the district, we have [(X1
- X)2 + (Y1
- Y)2]
for Euclidean distances]. Then, for the expected travel distance in
the district, we have
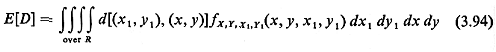
Note that the joint pdf for the coordinates of the
incident and of the
service unit can be made to reflect not only nonuniformities in the
distribution over R
but also possible dependencies between the locations of incidents
and of the service unit.
Expression (3.94) can be extended to the case
where N response units
are located in district R. Now let (Xi, Yi) indicate the location of
the ith response unit
(i = 1, 2, . . . , N) and (X, Y) the location of an incident. Then
the distance between
the incident and the closest response unit can be written
DN
= Min {d[(X1,
Y1,), (X,
Y)], . . . ,
d[(XN,
YN,), (X,
Y)]}
Since
DN, is then
a function of the random variables X, Y,
X1,
Y1,
X2,Y2,.
. . . , XN,
YN,
we can write
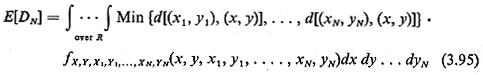
where fx, y,
x1,y1,...,xn,yn(x,y,x1, ....,
yn) is obviously the joint pdf for the coordinates of the incident
and the N response
units. Thus, in both (3.94) and (3.95) we have expressed expected
travel distance as the
expected value of a function of random variables whose joint pdf is
known. The problem of
computing the expected travel distance in the general case is,
therefore, no more (or
less) difficult than working with any other function of these random
variables (cf.
Section 3.1).
10
Obviously, in practice, there are severe
limitations on how far one can
go in deriving such exact expressions for E[D]. Problems become
mathematically intractable
as the number of random variables increases or as the shape of R
and/or the joint pdf for
the random variables becomes more complex. In many cases, however,
all is not lost as long
as one is willing to settle for good approximations rather than
exact results. This is
true any time the response units are stationary at known locations,
no matter what the
number, N, of these units is (and for practically any pdf for the
spatial distribution of
incidents/demands as well as for any shape of the district of
interest). It is also true,
for any value of N, in the case of mobile response units as long as
this approach can
also be generalized to expected distances to other than the closest
unit (e.g., to the kth
closest unit). subdistricts of responsibility have been defined in
such a way that each
sub-, district of R is served exclusively by a very small number of
mobile units
(preferably l!). In such instances, the following three-step
approach will always work:
STEP 1: Divide the district.R into several (possibly
many) nonoverlapping parts,
which we shall call "zones." Each zone must have
the following two
properties:
a. Its shape must be approximately rectangular, triangular,
circular, or any other
easy-to-work-with configuration.
b. The pdf for the spatial distribution of incidents/demands
within each zone must be
approximately uniform (or that pdf can be approximated by some
other sufficiently simple
expression as to permit easy mathematical manipulation).
STEP 2: Using the techniques of this chapter, compute all
intrazone and
zone-to-response unit expected distances, as required by the
problem at hand.
STEP 3: Multiply the expected distances computed in Step 2 by
appropriate probabilities
to obtain overall expected travel distances for district R.
Note that each zone in Step I can have an individual shape with
its "own" pdf
for the distribution of incidents. Note also that the greater the
degree of accuracy
desired, the larger the number of district zones should be (to
approximate better the
shape of the district R and the pdf for the spatial distribution of
incidents). In fact,
the three- step approach outlined above is very similar to the
approach that a computer
would follow in order to compute numerically the integrals in
expressions (3.94) and
(3.95). Rather than attempt a more formal
statement of the above
three-step approach, we now illustrate it through the following
example.
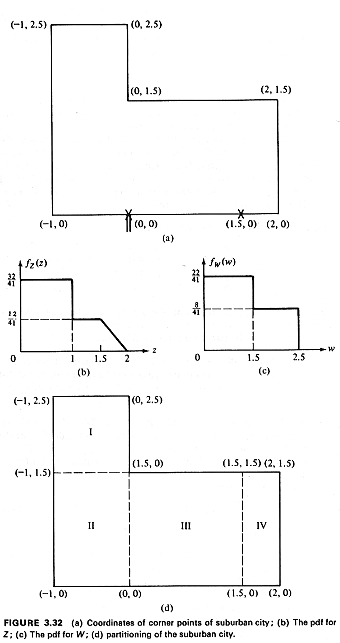
Example 14: Commuter Travel in a Suburban Town
Consider the suburban town shown in Figure 3.31. Its only
access to the central
business district (CBD) of the metropolitan area of which this
town is a part is through
the single bridge shown in Figure 3.3 1. The CBD is 6 miles from
the bridge's end, as
shown. Travel in the town is right-angle, as shown.
We are interested here in the total number of
person-miles traveled by
the town's working residents (not including schoolchildren) each
morning on their way to
work. (This. information might be useful in transportation
planning or in estimating
transportation-related fuel consumption by commuters.)
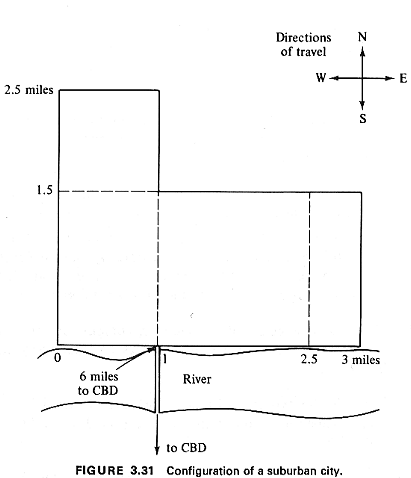
About 80 percent of the working
residents work in the
central city at the CBD. The other 20 percent work in town (and do
not have to cross the
bridge every morning). Trips are generated uniformly over the town
at the rate of about
2,000 trips per square mile. The only exception is the rectangular
area to the east of the
2.5-mile mark along the river (as shown in Figure 3.31), where the
density of trips
generated per square mile decreases linearly according to the
function g(d) = 4,000(3 -
d), where d is the east-west coordinate (2.5  or = d
or = d  or =
3) of each point as
measured from the southwesternmost point of the town (see Figure
3.31). There is no
difference between the spatial distributions of trip origins to the
CBD and to in-town
jobs. That is, of every 100 trips generated at each part of the
town, no matter where that
part is located, 80, on the average, are to the CBD and 20 to
in-town jobs. or =
3) of each point as
measured from the southwesternmost point of the town (see Figure
3.31). There is no
difference between the spatial distributions of trip origins to the
CBD and to in-town
jobs. That is, of every 100 trips generated at each part of the
town, no matter where that
part is located, 80, on the average, are to the CBD and 20 to
in-town jobs.
The spatial distribution (and density per square
mile) of in-town jobs
is assumed identical to the distribution ( and density) of
trip-generating points for
in-town jobs. (This may be the case, at least approximately, when
there are no
concentration of places of employment in a city and when no major
employers, such as
factories, etc., are located there.) For the purposes of this
example, we shall also make
the more questionable assumption that the job and residence
locations for in-town workers
are statistically independent (i.e., that knowledge of where an
in-town worker's home is
does not affect our a priori knowledge of where in town he or she,
and vice versa).
Solution
In working on this problem, we shal first compute
the expected travel
distance for CBD workers, then the expected travel distance for
in-town workers, and
finally the total passenger miles covered per day.
To start with, we need a coordinate system.
Although our choice of
origin does not really make much difference in this case, the edge
of the bridge on the
town's side is a particularly convenient one. We thus relabel the
various points of
interest according to this choice of origin, as shown in Figure
3.32a. we can also, using
the information given, construct the pdf for the spatial
distribution of trip-generation
points.

Note that fx,y(x,y) also
represents the pdf for
the spatial distribution of intown jobs according to the problem
statement.
With these preliminaries we can now compute:
1. E[D] for CBD workers. Since
the coordinates of the
edge of the bridge that travelers to the CBD must reach are (0,0),
the distance from any
point with coordinates (X, Y) to the bridge is given by D = |X| +
|Y|.
Exercise 3.10 Show that if we
define Z=|X| and W=|Y|,
then fz(z) and
fw(W) are as shown in
Figure 3.32b and c. Note that bothe pdf's can be derived almost by
inspection by first
obtaining fx(x) and
fy(y) from
fx,y(x,y).
In doing so we use the geometrical probability interpretation of
pdf's (cf. Section
3.4.1).
It is now easy to obtain
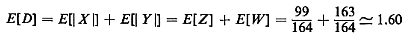
miles for the expected distance to point (0,0).
2. E[D] for in-town workers.
we now partition the
town into four non-overlapping zones, as
shown in Figure 3.32d.
We, wish, in effect, to compute E[D] between two random
points in the town with the
locations of each point determined independently, each according
to the pdf fx,y(x,y).
To do this we consider all possible intrazone and interzone
expected distances and then
multiply each expected distance by the appropriate
probability.
For instance, it can be seen that, given an
in-town worker:
P{both residence and place of work are in zone I}
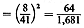
E[D | both residence and place of work are in zone
I] = 1/3 mile
Exercise 3.11 Show that if both the
residence and the
place of work of an in-town worker are in zone IV, his or her
conditional expected travel
distance is equal to 19/30 mile.
Exercise 3.12 By carefully
considering all residence and
place-of-work combinations, show that for in-town workers, E[D] =~
1.655 miles.
3. Total expected distance. A
total of about 10,250 trips
take place every morning. Of those 80 percent (= 8,200) are to the
CBD and 20 percent (=
2,050) are in-town. The expected travel distance to a CBD trip is
7.60 miles [remember
that point (0,0) is 6 miles from the CBD] while an in-town trip is
1.655 miles long on the
average. Therefore, the total expected distance traveled by
workers each morning is 65,755
person-miles.
It should be clear that the
problem of determining E[D]
for CBD workers was equivalent to computing E[D] between an incident
distributed as fx,y(x,y)
in the city and a fixed service unit located at the CBD. similarly,
E[D] for in-town
workers is equivalent to the expected travel distance between an
incident spatially
distributed as fx,y(x,y) in the town and a
mobile response unit
with that same distribution for its location in the town.
Finally, we might, out of curiosity, wish to
compare the result of
Exercise 3.12 for the expected travel distance for in-town workers
with the result that we
could have obtained had we used the approximate expression (3.84)
with c=0.67 (Table 3-1),
disregarding the fact that the shape of the town of interest is not
quite "fairly
compact and fairly convex" and that in a part of the town the
distributions of demand
and the "service unit" (i,e., of the job locations) are
not uniform. Since the
area of the town is 5.5 square miles, we have E[D] 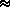 0.67 0.67 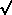 5.5 5.5 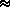 1.57 miles, for an error of
about 5 percent! The
reader who worked through Exercises 3.10-3.12 to obtain the exact
result of 1.655 will
definitely appreciate now the value of approxmate expression
(3.84). 1.57 miles, for an error of
about 5 percent! The
reader who worked through Exercises 3.10-3.12 to obtain the exact
result of 1.655 will
definitely appreciate now the value of approxmate expression
(3.84).
10
This approach can also
be generalized to expected distances to other than the closest
unit (e.g., to the kth
closest unit).
  
|


