3.10 Ratio of right-angle and Euclidean travel distances In this problem we test the reasonableness of the isotropy assumption used in Example 4. It is appropriate to question this assumption since most service regions in a city are such that 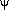will not be uniformly distributed between 0 and /2. We consider three cases.

b. Case 2. Suppose that the square-unit-area service area of part (a) is rotated at a 45° angle to the directions of travel. In such a case intuition might lead one to think that E[R] would be less than 4/. Why? To investigate this conjecture it is helpful to use the relationship

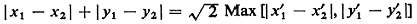
where the primed variables are defined relative to a coordinate system rotated at 45° with respect to the original coordinate system. Show that in such a case

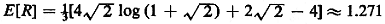
(Intuition is correct but the result is closer to 4/ than might otherwise have been expected.)

C. Case 3. Suppose that the mobile unit is located uniformly on the perimeter of a square rotated at 45° to the directions of travel. Suppose that the unit travels in a shortest (right-angle) distance manner to the center of the square. Again, T is the angle at which the directions of travel are rotated with respect to the straight line connecting the unit's initial position to the center of the square. Show that

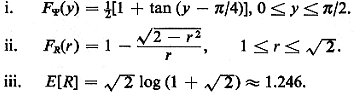
Do all the results for E[R] check with your intuition?