3.17 Cauchy random variable We recall from Section 3.3.3 that random variable X₁ has a Cauchy pdf if

a. Suppose that S₂ X₁ + X₂, where X₁ and X₂ are independent Cauchy random variables, each having pdf f_xi(.). Using the integral identity

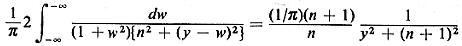
show that S₂ has a pdf 2/[(4 + y²)].

b. Proceeding by induction, show that

S_n X₁ + X₂ + . . . + X_n. (all X_i independent)

has a pdf n / [(n² + Y²)].

c. Thus, verify that the average of n independent Cauchy samples (i.e., V_n S_n / n) has a Cauchy pdf 1 / [(n² + Y² )]. Thus, "averaging together" a number of independent Cauchy samples yields a pdf for the average identical to that of any one of the individual samples. (This result contrasts sharply to most random variables, for which averaging of n independent samples reduces the variance by a factor of n^-1.)