3.29 Effect of traffic lights on
travel times A
vehicle travels a route from a to b, incurring a total travel
time
T = 6 +
W1 +
W2
(minutes)
where 6 = time to traverse
the distance (at
constant speed) from a to b
W1
= delay incurred at traffic ight 1
W2
= delay incurred at traffic light 2
As shown in Figure P3.29, the route is partitioned
into three 2-minute
travel-time segments. Each traffic light operates on a fixed cycle
of 1 minute green,
followed by I minute red. (We assume that no time is wasted in
decelerating and
accelerating, should one or two lights cause the vehicle to stop.)

Suppose that exactly at some prespecified time (say
12: 00 noon) we
examine the "phase" 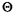 i, of each traffic
light (i = 1, 2). By definition, i, of each traffic
light (i = 1, 2). By definition,
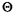 i = time until
light
i next turns to green (0 i = time until
light
i next turns to green (0  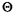 i < 2) i < 2)
For each light, we suppose that 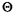 i,
is independently, uniformly distributed over [0, 2]. However,
once i,
is independently, uniformly distributed over [0, 2]. However,
once 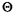 i
is known, its value isfixedfor all time. i
is known, its value isfixedfor all time.
Throughout this problem, we assume that departure
times at a occur
independently of the phases of the traffic lights.
a. Find the mean and variance of the travel time
from a to b.
b. Find the probability density function of the
travel time from a to b.
c. Let k = number of traffic lights at which the
vehicle is delayed. Find
the z-transform of the probability mass function for k.
For parts (d) and (e), only [not for parts (f)-(h)],
let
C = event that for the most recent vehicle
traveling from a to b, the
vehicle was stopped only at traffic light 1
d. Find the conditional joint probability density
function for 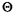 1
and 1
and 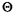 2,
given C. 2,
given C.
e. Find the conditional probability density
function for the travel time
from a to b for the next vehicle to travel from a to b, given C.
(Assume that you know
nothing about when the next vehicle will leave a.)
For parts (f)-(h), suppose that vehicles leave a in
a Poisson manner with
mean 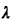 = 1 vehicle per minute. Vehicles occupy zero space and, when
in a traffic light
queue, accelerate and decelerate instantaneously together.
= 1 vehicle per minute. Vehicles occupy zero space and, when
in a traffic light
queue, accelerate and decelerate instantaneously together.
f. Is the vehicle arrival process at b a
Poisson process? Why or
why not?
g. Determine the mean and variance of the queue
length (number of
vehicles) at traffic light I at the instant before the light turns
green. (This is a
primer for Chapter 4.)
h. A traffic engineer adjusts the phases of the
two traflac lights so that
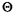 1
= 1
= 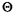 2
= 0 (relative to 12: 00 noon). Suppose that at 12: 00 noon we are
given conditional
information that no vehicles have left a during the last
8 minutes. Carefully
sketch and label the probability density function for the time of
arrival at b of the next
vehicle to arrive there. 2
= 0 (relative to 12: 00 noon). Suppose that at 12: 00 noon we are
given conditional
information that no vehicles have left a during the last
8 minutes. Carefully
sketch and label the probability density function for the time of
arrival at b of the next
vehicle to arrive there.
|