4.6.5 Extensions and Variations
Further extensions and variations of the many cases discussed in
this section can be developed by permitting the arrival rates and/or the service rates to
take the form
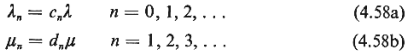
where 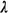 and
and  are
constants and c. and d. are coefficients that depend on the state of the queueing system.
(Usually, co = 1 and d1,
= 1, so that are
constants and c. and d. are coefficients that depend on the state of the queueing system.
(Usually, co = 1 and d1,
= 1, so that 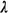 reflects the rate of demand arrivals when the queueing system is empty and
reflects the rate of demand arrivals when the queueing system is empty and  the rate of service
when there is only one user in the queueing system.) the rate of service
when there is only one user in the queueing system.)
Through (4.58a), one can take into account often-observed phenomena
such as reneging and balking. Balking refers to cases in which a prospective user
of the queueing system decides, upon arrival at the system and observation of its state,
not to wait for its use but (perhaps) to go elsewhere. Reneging is the phenomenon
in which users who have already joined the queue become discouraged after a while
and leave without obtaining service.
Similarly, by an appropriate choice of a functional form for dn,
one can account for such phenomena as the often-observed "speed up" of service
by human operators whenever queues grow very long. It is easy to imagine how reneging,
balking, service speed up or, even, service slowdowns could occur in connection with our
emergency center example.
Commonly used forms of cn
include cn = (n + j)-a and dn.
= nb, where a and b are positive constants. Note
how by adjusting a and/or b one can model several types of user behavior. These can be
applied with single- or multiserver systems whose capacity is finite or infinite. Although
it is usually impossible to obtain closed-form expressions for such quantities as Pn,
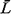 , ,  , and so on, for
these systems, it is often relatively easy to solve numerically the balance
equations and tabulate the numerical results (see also Problem 4.2). Such tabulations have
been published by several researchers. , and so on, for
these systems, it is often relatively easy to solve numerically the balance
equations and tabulate the numerical results (see also Problem 4.2). Such tabulations have
been published by several researchers.
|