4.9 Queueing Systems With Priorities
In all the cases that we have discussed so far, the order in which the users of a service
facility get access to that service facility has been determined by queue disciplines such
as FCFS, LCFS, and SIRO (see also Section 4.2). A common
feature of these disciplines is that users are characterized by the order of their arrival
at the queueing system, but no distinction is made among different classes of
users with reference to the type or the length of service they request. It is natural to
ask what effect these disciplines have on the expected total system time,
 (or on (or on  q,
or q,
or 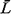 or or 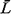 q,),
experienced by users of a queueing system. q,),
experienced by users of a queueing system.
Suppose, for example, that in the case of the
single operator with an infinite number of lines at the center for emergency calls which
we discussed earlier (Section 4.6), one wanted to choose among the FCFS, SIRO,
and LCFS disciplines. To maintain a FCFS (or LCFS)
sequencing of calls, it is necessary to purchase an electronic call-sequencing device.
Does such a device contribute anything to improving the quality of service as perceived by
callers to our emergency center?
To answer this question, one can reexamine the
analysis that led to (4.38), the expression for  for that M/M/1 system with infinite capacity. Note
that the state-transition diagram of Figure 4.6 is unaffected by the queue discipline in
use-all that matters is the total number of calls on hand. Thus, the analysis leading to
(4.38) is identical for FCFS, SIRO, and LCFS, and
consequently, at least for this example, for that M/M/1 system with infinite capacity. Note
that the state-transition diagram of Figure 4.6 is unaffected by the queue discipline in
use-all that matters is the total number of calls on hand. Thus, the analysis leading to
(4.38) is identical for FCFS, SIRO, and LCFS, and
consequently, at least for this example,
 FCFS = FCFS =  LCFS
= LCFS
=  SIRO
(4.98) SIRO
(4.98)
Moreover, since Little's formula (4.10) is valid for
any queue discipline (see Section 4.4), the same is true for 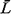 , , 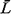 q, and q, and  q. q.
Does this mean that callers will be indifferent
to the queue discipline? Probably not, for the distributions of the total system
times and of the waiting times (but not of the number of calls in the system or in queue)
will be different in the three cases. To understand why, consider a random caller who at
the instant when she is connected with the emergency center is told that k other callers
are also waiting for service, while the operator is currently busy with another call. In a
FCFS queue this information is valuable to the new caller in estimating her expected
waiting time, in a SIRO queue less so, and in a LCFS queue it is practically useless. We
infer from the above that, for this example,
Var (WFCFS) < Var (WSIRO)
< Var (WLCFS)
(4.99)
where Var (W) denotes the variance of the total system occupancy time.
One can extend the same reasoning that led to
(4.98) to any queueing system, and indeed the following statement can be made [KLEI 76]:
As long as the queueing discipline sequences the users of a queueing system in a way that
is independent of their service time (or any measure of their service time), the
distribution of the number in the system-and the expected total system time and waiting
time-will be invariant to the queue discipline.
Note that the foregoing statement applies to other conceivable queue disciplines in
addition to FCFS, SIRO, and LIFO.
The validity of (4.99) for any queueing system
can also be argued intuitively (the inequalities become equalities for systems with an
infinite number of servers). However, in all but a few cases-such as the M/G/1 system-it
is very difficult to obtain Var (WSIRO) or Var (WLCFS),
even with advanced techniques.
In practice, though, numerous queueing systems
sequence the access of users to service facilities by using criteria related to the length
of service or to the type of service requested. The latter criterion (type of service
requested) is particularly often used in the case of urban services and, especially, of
emergency urban services. For instance, police car dispatchers almost always classify
reported incidents into one of several categories and accord higher priority to some
categories over others (e.g., calls about "crimes in progress" receive more
immediate attention than reports of "missing, probably stolen items").
Similarly, in emergency medical rooms of large hospitals, certain types of patients are
given higher priority than other types. We shall examine next the queueing characteristics
of systems of this type.
|