4.14 Police helicopters and police cars Assume that in a circular city with a radius of R miles, calls for police service are generated in a Poisson manner at the rate of 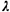per hour per city square mile. Calls are uniformly distributed over the city.
        The police department is contemplating the purchase of k helicopters to respond to certain types of police calls. The helicopters will be flying straight to the location of each incident, at an effective speed of v_H, miles/hr.
        The special police cars that are presently used for these calls have an effective speed of v_c, miles/hr and travel in right- angle distances. The city is rather large and its streets have no particular orientation with respect to the coordinate axes.
         The dispatching strategy that the police controller uses, whether operating a helicopter-based or a car-based system, is the following. Whenever all service units are busy, calls for police assistance are placed in a first-come, first-served, infinite capacity queue and the first service unit which becomes available is immediately dispatched to the first call in the queue. If, on the other hand, more than one service unit is available, the dispatcher selects one of the available units randomly (with no consideration to service unit locations) and dispatches it to the next call.
        It is also known that the durations of service for incidents serviced by helicopters or by cars, after arrival on the scene, are random variables with negative exponential distributions with average service time equal to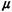 1/_H and 1/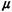_c, respectively. The durations of service to successive incidents are statistically independent.
        Finally, it is known that a unit that completes service to a call remains stationary until it is dispatched to a new incident.

a. Make the assumption that travel times to successive incidents for any given service unit are statistically independent. Also assume steady-state conditions.           Let the criterion for comparison between the k helicopter system and the m police car system be that fraction of time that a randomly selected service unit is busy (a server is considered busy if it is either traveling to the scene of an incident or servicing a call at the scene). Find the value of m for which the car-based system will most closely match the helicopter system for any given number k of helicopters.           Your answer should be an expression for m containing only variables defined above and constants. Please explain your work.

b. For R = 4, v_H = 80 mph, v_c = 25 mph, and 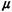_H = 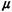_c, = 4 calls per hour, compute the ratio m/k for your answer in part (a).

c. In part (a), we assume that travel times to successive incidents for any given service unit are statistically independent.
        Is this assumption a correct one? Please explain briefly and clearly in intuitive terms.

d. Assume now that there are two helicopters (and no police cars in the district). Also assume that R/v_H << 1/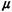_H. Find a good approximation for the probability that, with the system in the steady state, an observer arriving at a random instant will find both helicopters busy and exactly one call waiting in the queue. For what condition is your answer true?

e. Under the assumptions of part (d), find the probability that with the system in the steady state, the two helicopters will complete service to exactly l calls during a time interval T.