5.5.2 Workload Estimation
The last conjecture brings us to feature 4 of the entire
approximation procedure, in which we obtain a set of N
simultaneous equations relating the N unknown 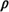 n's to the dispatch policy and the
arrival rates from the various geographical atoms. Suppose that we again
equate the mean service time to unity (i.e., n's to the dispatch policy and the
arrival rates from the various geographical atoms. Suppose that we again
equate the mean service time to unity (i.e., 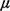 -1 = 1), thus making the unit of time equal
to one mean service time unit. Then, the net rate
Rn at which server n is assigned to customers,
measured over a very long time period, is equal to the workload -1 = 1), thus making the unit of time equal
to one mean service time unit. Then, the net rate
Rn at which server n is assigned to customers,
measured over a very long time period, is equal to the workload 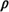 n of server n. Thus, if we
can determine a value for Rn, we have determined a
value for n of server n. Thus, if we
can determine a value for Rn, we have determined a
value for 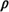 n. We describe
mathematically the dispatch preference policy by defining the
following: n. We describe
mathematically the dispatch preference policy by defining the
following:
Gnj  | set of geographical atoms for which
server n is the jth preferred dispatch alternative, n,
j = 1, 2, . . . N |
maj  |
identification number of the jth preferred server for atom
a |
For instance, if G23 = {7, 8, 10, 12},
server 2 is the third preferred dispatch alternative for atoms 7, 8, 10,
12 and, for instance, m7 3 = 2. Now an exact
expression for Rn can be written as follows:
Rn = 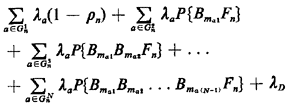 |
(5.50) |
where the term 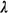 D accounts
for delayed dispatches from a queue, which are apportioned equally among
all N servers; thus, D accounts
for delayed dispatches from a queue, which are apportioned equally among
all N servers; thus,
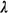 D = D = 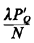 (assuming an infinite-capacity queue) (assuming an infinite-capacity queue)
In words, (5.50) states that the net rate at which server n is
assigned to customers is equal to (1) the rate at which customers arrive
from server n's primary response area, multiplied by the fraction
of time server n is available to start servicing such customers
immediately; plus (2) the rate at which customers arrive from
server n's second-preferred areas, multiplied by the fraction of
time that both the first preferred server is busy and server
n is available to start servicing such customers immediately;
plus (3) similar terms for the remaining j-preferred
areas; plus (4) a term that apportions equally to all servers a
fraction (1/N) of customers delayed in queue.
Given our approximation conjecture, we can simplify (5.50) by
estimating the dispatch probabilities as products of utilization or
availability factors and the appropriate correction term. For instance,
we approximate
P{B3B6F5}
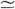 Q(N, Q(N, 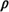 ,
2) ,
2) 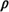 3 3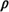 6 6 (1 - (1 - 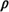 5). Given this approximation and
substituting Rn = 5). Given this approximation and
substituting Rn = 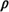 n, we can rewrite (5.50) as n, we can rewrite (5.50) as
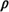 n = n =  |
(5.51) |
We notice that each of the summation terms on the right-hand side of
(5.51) contains (1 - 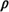 n) as a
factor. If we remove this factor, then the sum of these N terms
is not a function of n) as a
factor. If we remove this factor, then the sum of these N terms
is not a function of 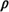 n, a
desirable property in an iterative procedure whose purpose is to compute
an estimate for n, a
desirable property in an iterative procedure whose purpose is to compute
an estimate for 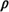 n. n.
RnF  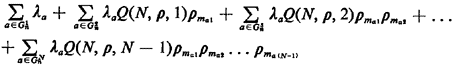 |
(5.52) |
has an intuitive interpretation. It is the (approximate) customer
assignment rate for server n during periods when server n
is free. Simple manipulation of (5.51) yields
 n = n = 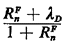 |
|
n = 1, 2, . . . , N |
(5.53) |
Here we assume that 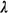 D <
1, implying that D <
1, implying that 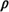 n < 1;
otherwise, the system would be overloaded. Equation (5.53) [together
with (5.52)] represent a set of N simultaneous nonlinear
equations relating the N unknowns n < 1;
otherwise, the system would be overloaded. Equation (5.53) [together
with (5.52)] represent a set of N simultaneous nonlinear
equations relating the N unknowns 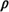 n, n = 1, 2, . . . ,
N. They can be solved iteratively to obtain values for each of
the n, n = 1, 2, . . . ,
N. They can be solved iteratively to obtain values for each of
the 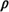 n's. A specific iterative
algorithm is displayed in Figure 5.19. As you will discover in Problem
5.12, (5.53) yields a very reasonable approximation for the workload
even on the first iteration (in which all workloads on the righthand
side of the equation are set equal). Rarely are more than three or four
iterations required for even very stringent convergence criteria. n's. A specific iterative
algorithm is displayed in Figure 5.19. As you will discover in Problem
5.12, (5.53) yields a very reasonable approximation for the workload
even on the first iteration (in which all workloads on the righthand
side of the equation are set equal). Rarely are more than three or four
iterations required for even very stringent convergence criteria.
|


