|
5.10 Hypercube approximation procedure for the
zero-line-capacity case Suppose that we wish to derive an
approximate procedure for finding the performance measures of the
hypercube model, analogous to that of Section 5.5, but assuming zero
line capacity. To do this, we must develop a new Q factor and new
workload normalization conditions.
- Verify that the appropriate steady-state probabilities for the
corresponding M / M / N zero line capacity queue are

where 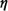 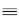 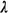 /N < + /N < +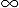 (Assume that (Assume that
 = 1) = 1)
- Confirm that the average utilization factor is

- Now we would like to develop a correction factor
Q'(N,
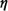 , j) that, when multiplied
by , j) that, when multiplied
by  j(1 - j(1 -  ), gives the exact probability
P{B1B2. .
.BjFj+1} for the M
/ M / N zero line capacity system. Following reasoning analogous to
Problem 5.9, verify that ), gives the exact probability
P{B1B2. .
.BjFj+1} for the M
/ M / N zero line capacity system. Following reasoning analogous to
Problem 5.9, verify that

and where Q*(N, 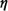 ,
j) is equal to Q(N, ,
j) is equal to Q(N, 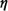 ,
j)as computed for the M / M / N infinite line capacity
case, but with P{So} replaced by
P'{So} ,
j)as computed for the M / M / N infinite line capacity
case, but with P{So} replaced by
P'{So}
- Conclude that an appropriate workload approximation procedure for
the zero-line-capacity case would utilize (5.52), (5.53), and the
algorithm of Figure 5.19, with Q( ) replaced by Q'( ) and
with the following other modifications:

|


