6.2.3 Traffic Assignment Problem
A simple application of shortestt-path techniques occurs in the
preliminary determination of the traffic loads to be expected on different
segments of a transportation grid. To make this determination, an
origin-destination traffic matrix is required for the network of interest.
Passengers are then assumed to follow the least distance (or time or cost)
path from origin to destination through the network. The levels of flow on
all links of the network are then computed by:
- Using some algorithm to find the shortest paths between all pairs of nodes.
- Adding, for each origin-destination pair i-j, the traffic flow t(i, j)
to the flow on every link in the shortest path from i to j.
Example 3
Consider again the network of Figure 6.6. Assuming that the
origin-destination data are as shown below, find the traffic flow on the
links of the graph.
Origin-destination matrix (in tens of vehicles per hour):
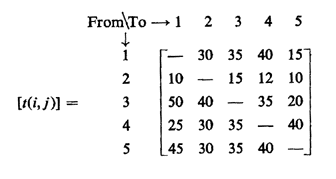
Solution
We have already obtained all shortest paths for this graph and recorded
them in the matrix P(5) (see Section 6.2.2). We can then determine
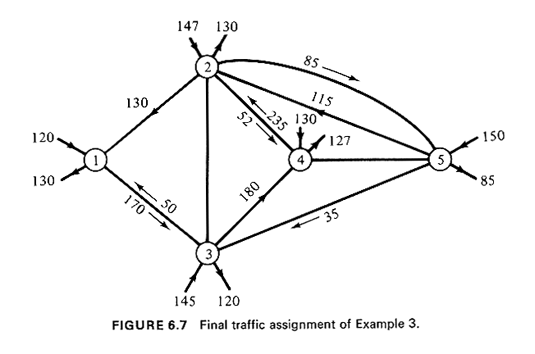
the traffic flow on each link of the graph, as shown in Figure 6.7. To better
understand the computation of the various flows, consider the flow of 52
units on the undirected link (2, 4) and in the direction from 2 to 4. rne
1ink (2, 4) in the 2 -----> 4 direction is part of the shortest path from
node 2 to node 4 and from node 5 to node 4. Therefore, the traffic for these
two destination pairs (i.e., 12 and 40 units, respectively) will use the
(2, 4) link in the 2 ----> 4 direction, hence the flow of 52 units.
Note that there are traffic flows in both directions through some
undirected links and that other (directed or undirected) links remain
completely unused as indicated by the absence of any traffic flow numbers
next to them. Finally, note the conservation of traffic at each node of
the network.
This type of traffic flow determination can be useful in determining the
capacity requirements for an urban transportation network at the initial
stages of planning or as long as the network is relatively free of
congestion. It is much less useful and meaningful in predicting traffic
flows for a transportation network that has already been built and is
heavily utilized. This is so because the determination of traffic flows,
as performed above, ignores the facts that:
- Shortest distance--or, shortest travel time--is not the sole criterion
for route selection.
- The capacity of any link on a transportation system is finite.
- Because of 2, travel speeds are a function of the amount of congestion
on a transportation link and, as a result, the determination of the shortest
paths cannot be made independently of traffic-flow determination.
In particular, the effects of congestion call for more sophisticated
approaches than the above in determining traffic flows. These approaches
are generally referred to as "traffic assignment" techniques. Good general
references about these techniques can be found in [FLOR 76]. (See also
Problem 4.10 for the differences between "user-optimum" and "system-optimum"
traffic assignment.)
|



