6.4.12 Single-Depot VRP

We shall examine next the following version of the vehicle routing problem. Let there be n demand points in a given area, each demanding a quantity of weight Q_i (i = 1, 2, . . . , n) of goods to be delivered to it (goods are assumed indistinguishable but for their weight). The goods in question are stored at a depot, D, where a fleet of vehicles is also stationed. Vehicles have identical maximum weight capacities and maximum routetime (or distance) constraints. They must all start and finish their routes at the depot, D. The problem is to obtain a set of delivery routes from the depot, D, to the various demand points to minimize the total distance covered by the entire fleet. It is assumed that the weights Q_i (i = i , . . . , n) of the quantities demanded are less than the maximum weight capacity of the vehicles and we require that the whole quantity Q_i demanded at a given point i be delivered by a single vehicle (i.e., we do not allow for the possibility that one third, say, of Q_i will be delivered by one vehicle and the remaining two thirds by another).

Obviously, the words "supply" and "quantity supplied" can be substituted for "demand" and "quantity demanded," in which case the depot becomes a collection point. Thus, the VRP applies equally well to solid waste collection from a specific set of points and to parcel delivery to a set of points. A notable recent application, for instance, has been in routing of newspaper distribution vehicles delivering editions of a well-known newspaper to newsstands in an urban area [GOLD 77].

We also note that in specific applications of the VRP, either the maximum weight or the maximum route-time constraints may be relaxed. However, both usually play a role. For instance, in the newspaper delivery problem just mentioned, one constraint, in addition to the maximum number of newspapers that a vehicle can carry, was that all deliveries to newsstands must be made within an hour of press time.

When neither constraint applies, the VRP reduces to a traveling salesman problem: if the objective is simply to minimize total distance, it is a 1-TSP [from (6.10)]; if the number of vehicles to be used is specified, it is a m-TSP. It can thus be seen that TSP's can be viewed as special cases of VRP's. By inference, VRP's can be expected to be more difficult than TSP's as far as optimum solutions are concerned. Indeed, although several versions of VRP's have been formulated as mathematical programming problems by various investigators, the largest vehicle routing problems of any complexity that have been solved exactly reportedly involved less than 30 delivery points [CHRI 74]. By contrast, the heuristic approaches that we shall describe next can be used even with thousands of delivery points.

Heuristics for the single-depot VRP. By far the best-known approach to the VRP problem is the "savings" algorithm of Clarke and Wright. Its basic idea is very simple. Consider a depot D and n demand points. Suppose that initially the solution to the VRP consists of using n vehides and dispatching one vehicle to each one of the n demand points. The total tour length of this solution is, obviously, 2 d(D, i).

If now we use a single vehicle to serve two points, say i and j, on a single trip, the total distance traveled is reduced by the amount

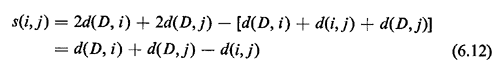
The quantity s(i, j) is known as the "savings" resulting from combining points i and j into a single tour. The larger s(i, j) is, the more desirable it becomes to combine i and j in a single tour. However, i and j cannot be combined if in doing so the resulting tour violates one or more of the constraints of the VRP.

The algorithm can now be described as follows.

Clark>Wright Savings Algorithm (Algorithm 6.7)

STEP	1:	Calculate the savings s(i, j) = d(D, i) + d(D, j) - d(i, j) for every pair (i, j) of demand points.
STEP	2:	Rank the savings s(i, j) and list them in descending order of magnitude. This creates the "savings list." Process the savings list beginning with the topmost entry in the list (the largest s(i, j)).
STEP	3:	For the savings s(i, j) under consideration, include link (i, j) in a route if no route constraints will be violated through the inclusion of (i, j) in a route, and if: a. Either, neither i nor j have already been assigned to a route, in which case a new route is initiated including both i and j. b. Or, exactly one of the two points (i or j) has already been included in an existing route and that point is not interior to that route (a point is interior to a route if it is not adjacent to the depot D in the order of traversal of points), in which case the link (i, j) is added to that same route. c. Or, both i and j have already been included in two different existing routes and neither point is interior to its route, in which case the two routes are merged.
STEP	4:	If the savings list s(i, j) has not been exhausted, return to Step 3, processing the next entry in the list; otherwise, stop: the solution to the VRP consists of the routes created during Step 3. (Any points that have not been assigned to a route during Step 3 must each be served by a vehicle route that begins at the depot D visits the unassigned point and returns to D.)

Example 13: Refuse-Collection, Revisited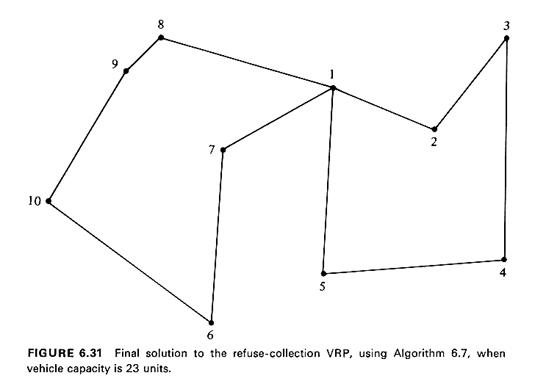

Consider once again the 1O-point refuse-collection problem examined earlier (Example 9). The depot is node (point) 1 and the nine points to be visited are now recognized to pose different requirements in terms of the expected quantity of refuse to be collected on each daily tour. The pertinent distance and savings data are shown in Table 6-4. Because the distance matrix is symmetric,

the distances d(i, j) and the savings s(i, j) can both be exhibited in a single 9 x 10 matrix (no savings are associated with the depot, i.e., node 1). In Table 64, the savings s(i, j) are shown above the diagonal. For instance,

    s(4, 6) = d(1, 4) + d(1, 6) - d(6, 4) = 57 + 61 - 71 = 47 

Table 6-5 lists the quantities of refuse to be collected from each of the nine nodes 2 through 10. We assume that the capacity of each vehicle is equal to 23 units and apply the third step of the Clarke-Wright algorithm to the savings list, as shown in Table 6-6. No constraint other than the maximum capacity one is assumed to exist.

The processing of the savings list now proceeds as follows. The largest savings is associated with link (6, 10), so a tour consisting of {1, 6, 10, 1} is created. The second entry in the list is associated with link (9, 10). The initial route is therefore expanded to {1, 6, 10, 9, 1} since the conditions under Step 3 are satisfied by such an expansion. Next is the entry for link (8, 9) and expansion of the route to {1, 6, 10, 9, 8, 1} also turns out to be acceptable. However, expansion to {1, 5, 6, 10, 9, 8, 1}, as suggested by the next entry for link (5, 6), is impossible since such a route would imply a load of 24 units (> 23). Thus, link (5, 6) is rejected. So is link (8, lO)--both 8 and 10 are already in the tour; and (7, lO)--since 10 is interior to the tour. The appearance of link (4, 5) as the next entry in the savings list leads to formation of another tour {1, 4, 5, 1}. Next, the inclusion of point 7 in the first tour is acceptable and that tour is expanded to {1, 7, 6, 10, 9, 8, 1} with a load of 23 (meaning that this tour cannot be expanded further).

Proceeding in the sate way, points 3 and then 2 are successively added to the second tour, ending up with the tour {1, 2, 3, 4, 5, 1}, with a load of 19 units. Since all points have been included in a tour, that also means the completion of our procedure. The two tours are shown in Figure 6.31 and their combined length (total distance traveled) is 397 units.

As the reader may have already surmised, the Clarke-Wright algorithm can be programmed to run very efficiently and, since it involves very simple manipulations of the data set, it can be used with large problems. Because

nodes are added to routes one or two at a time, an additional advantage of the algorithm is that it is possible to check whether each addition would violate any set of constraints, even when that set is quite complicated. For instance, besides the constraints on maximum capacity and maximum distance, other constraints might be included, such as a maximum number of points that any vehicle may visit.

On the other hand, there is no guarantee that the solution provided by such a naive algorithm will be anywhere close to the optimum. While experience has shown that the algorithm performs quite well most of the time, it is possible to devise "pathological" cases for which the Clarke-Wright solutions are very poor indeed. However, it is often possible to improve considerably, by inspection, a set of VRP tours produced by the savings algorithm. In fact, a powerful interactive "man-machine" approach has been developed for that purpose [KROL 72. In this approach, a computer "suggests" a solution using the savings algorithm and projects that solution on a television screen. The human operator then attempts to improve on this solution using his/her knowledge of the problem as well as such geometrical properties of good tours as those we have already discussed for the Euclidean TSP (Section 6.4.8). The operator, using a light pen, suggests these improvements to the computer, which, in turn, comes up with a new solution to the VRP; and so on.

Example 13 (continued)

Consider again the nine-point refuse-collection problem of the previous example and suppose that we make a single change in the earlier problem by setting vehicle capacity to 16 units (instead of 23).
Solution

The reader may wish to verify that the solution produced through the savings algorithm now becomes:

This solution is shown in Figure 6.32. By observing that tours are partially included in each other and that they intersect three times, we are led to attempt some modifications seeking an improvement on the earlier solution.

A natural modification to attempt, for instance, is the following:

This solution is both feasible and covers 11 percent less distance than the initial Clark-Wright solution (Figure 6.33).

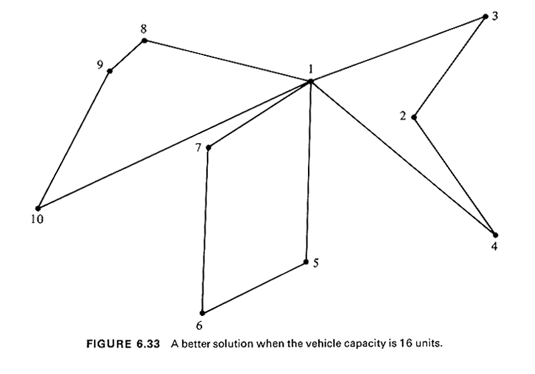
Several alternatives to the Clarke-Wright algorithm have been proposed. One that seems to produce good solutions to VRP,s can be summarized as follows [GILL 74b].

Sweep Algorithm for the VRP (Algorithm 6.8)

Assume that polar coordinates are available for all points to be visited by the vehicles (the depot, for instance, might be used as the origin in the coordinate system). The points then can be ordered in terms of increasing angle by sweeping (clockwise or counterclockwise) a ray initially drawn from the depot to some arbitrary point--known as the seed point. Routes are then drawn up by adding demand points to a route as these demand points are swept: beginning at the seed (whose angle can be set to 0), points are included in a route as they are swept, until the load capacity of a vehicle precludes addition of the next point swept to the current route. That point then becomes the seed for the next route and the process is completed when all points have been swept (i.e., included in a route). Once the points that form each route are available, a TSP algorithm can be used to determine the order of point traversal for each individual route. Thus, the sweep algorithm is a good example of the "cluster first, route second" approach.

Example 13 (continued)

The improved solution (total distance covered = 461 units, Figure 6.33) obtained in the last exampl~with a vehicle capacity of 16--would have resulted from the sweep algorithm had we designated point 3 as the seed point and then swept the other eight points in a clockwise direction.

The major disadvantage of the sweep algorithm is that it does not generate the vehicle tours as it processes the nodes. This is done only after the nodes that constitute each tour have been specified and thus becomes a time-consuming procedure. In addition, whenever there are constraints on the maximum tour lengths as well, some clusters may prove to lead to tours that are unacceptably long. Finally, the algorithm requires Euclidean distances and satisfaction of the triangular inequality throughout.

In general, the Clarke-Wright algorithm seems to enjoy an advantage in terms of both efficiency and flexibility over other available VRP algorithms and has been used extensively. The method has been programmed as the VSPX (Vehicle Scheduling Program) package by IBM and is thus available commercially. The algorithm can be rendered even more powerful through a simple modification that forces the algorithm to generate several alternative solutions and through careful organization and storage of the information it utilizes [GOLD 76].