6.4.4 Solving the Chinese Postman's Problem

We now return to the Chinese postman,s problem and solve the problem of finding the minimum length, edge-covering tour of a graph G(N, A) with no restrictions placed on G other than that it be connected and undirected.

The solution procedure consists of adding, in a judicious manner, artificial edges, parallel to the existing ones, to the original graph G to obtain a new graph G¹(N, A¹) on which an Euler tour can be drawn. This means that the addition of the artificial edges should be such as to turn all odd-degree nodes on G into even-degree nodes on G¹. Moreover, this should be accomplished by selecting that combination of artificial edges which results in the minimumlength tour at the end. The addition of an artificial edge in parallel to an existing one in the original network simply means that the existing edge will have to be traversed twice in the final Chinese postman,s tour.

An important observation is helpful at this point.

Lemma: The number of nodes of odd degree in an undirected graph G is always even.

Exercise 6.5 Prove the lemma.

Hint: The sum of the degrees of all the nodes in G is an even number since each edge is incident on two nodes.

We now describe the solution approach in general terms:

Chinese Postman Algorithm--Undirected Graph (Algorithm 6.5)

STEP 1	Identify all nodes of odd degree in G(N, A). Say there are m of them, where m is an even number according to the lemma.
STEP 2	Find a minimum-length pairwise matching (see below) of the m odd-degree nodes and identify the m/2 shortest paths between the two nodes composing each of the m/2 pairs.
STEP 3	For each of the pairs of odd-degree nodes in the minimum-length pairwise matching found in Step 2, add to the graph G(N, A) the edges of the shortest path between the two nodes in the pair. The graph G1(N, A1) thus obtained contains no nodes of odd degree.
STEP 4	Find an Euler tour on G1(N, A1). This Euler tour is an optimal solution to the Chinese postman,s problem on the original graph G(N, A). The length of the optimal tour is equal to the total length of the edges in G(N, A) plus the total length of the edges in the minimum-length matching.

A pairwise matching of a subset N' N of nodes of a graph G is a pairing of all the nodes in N' (assuming that the number of nodes in N' is even). A minimum-length pairwise matching of the nodes in An is then a matching such that the total length of the shortest paths between the paired nodes is minimum.

Example 7: Application of Algorithm 6.5

Consider the graph of Figure 6.15a. The numbers on the edges indicate the lengths of the edges. The graph contains four nodes of odd degree (a, b, d, and e). Thus, there are three possible matchings of the odd-degree nodes: a-b and d-e; a-d and b-e; and a-e and bad. Th e augmented networks that would result from the addition of the artificial edges corresponding to each of these three matchings are-shown in Figure 6.15b-d, respectively. Of the three matchings, the optimal is obviously the one shown in Figure 6.15c. It adds only 12 units of length to the tour as opposed to 16 for Figure 6.15b and 20 for 6.15c. Thus, the graph shown on Figure 6.15c should be the result of the procedure outlined in Steps 2 and 3 of Algorithm 6.5. Supposing that the required tour must begin at node a, a solution to the Chinese postman,s problem for the graph of Figure 6.15a is the tour {a, d, a, c, d, e, c, b, e, b, a}. Its total length is 60 units, of which 48 is the total length of the graph 6.1 5a, while 12 units are due to the artificial edges. In other words, edges (a, d) and (b, e) will be traversed twice.

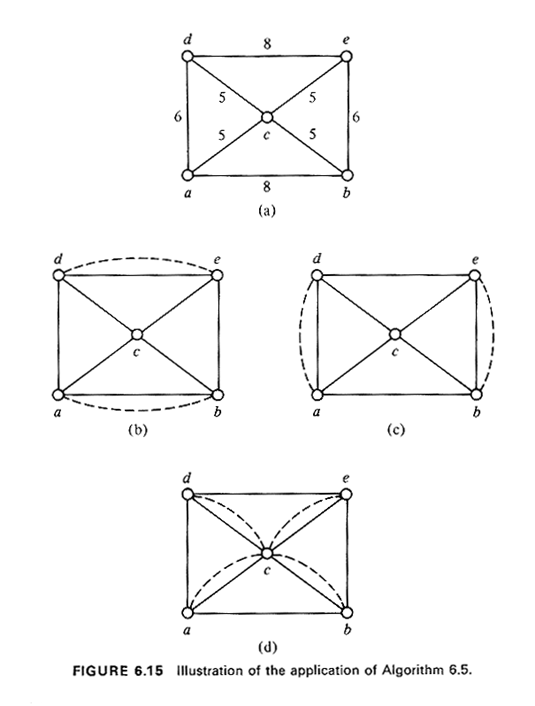
In Algorithm 6.5, we have concentrated exclusively on the shortest paths between pairs of odd-degree nodes. That this should be so can be seen as follows. Were a supposedly optimal pairwise matching between odd-degree nodes to contain a path, P¹, between any given pair of nodes that is not the shortest path, P. between these two nodes, the solution could be improved by simply substituting P for P¹ in the drawing of the artificial edges, since the length of P is, by definition, smaller than the length of P¹.

In reviewing Algorithm 6.5, we can see that its only difficulty lies in Step 2, since Steps 1, 3, and 4 are all very simple. For Step 2, however, the number of possible pairwise matching combinations increases very quickly with the number of odd-degree nodes. Some thought will show that with m odd degree nodes in G (remember that m is always even), there are

possible distinct pairwise matching combinations. Thus, for m = 4, there are I · 3 = 3 possible combinations (as we have already seen in our last example), for m = 10,945 combinations, and for m = 20, about 655 million combinations.

Fortunately, an efficient, but quite complicated algorithm for minimum length matchings on undirected graphs is now available. This algorithm is based on the theory of matching on graphs that has been developed in recent years primarily by J. Edmonds. The interested reader is referred to [EDMO 73] or to [CHRI 753 for its details. Here we only note that the algorithm is an exact one (i.e., finds the optimum matchings) and efficient computer-implemented versions solve the problem in time proportional to n³, where n is the number of nodes in the graph under consideration. The algorithm not only finds the minimum-length matchings but also identifies the shortest path associated with each pair. It follows that in the worst case Algorithm 6.5 is also O(n³).

Manual approach to matching. When Edmonds' minimum-length matching algorithm is used in Step 2 of Algorithm 6.5, an optimum solution to the Chinese postman,s problem is obtained. Experience has shown, however, that whenever the Chinese postman problem is posed in a geographical context (and this of course is the case in urban service systems applications), then excellent--in the sense of being very close to the optimum--manual solutions can be obtained practically by inspection with the aid of a good map. The map can be used to perform all four steps of Algorithm 6.5, and the only step where one risks deviating from the optimum solution is in finding the minimum-length matching in Step 2.

The manual search for an approximately minimum-length matching of odd-degree nodes in Step 2 is greatly aided by the following key observation:

In a minimum-length matching of the odd-degree nodes, no two shortest paths in the matching can have any edges in common.

To see this, consider Figure 6.16, assuming that nodes a, b, c, and d are all of odd degree and that the shortest paths between, say, the pairs of nodes a-c and Kd have edge (p, q) in common. Then it is impossible that the minimum-length pairwise matching contain the pairs a-c and Fd, since it would then be possible to obtain a better (shorter) matching by coupling

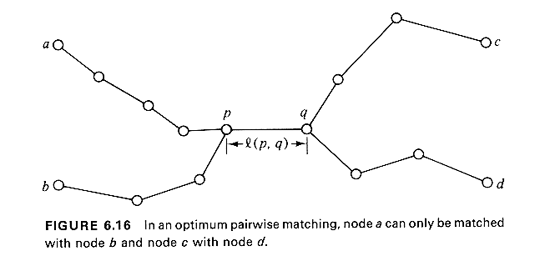
together nodes a and b into one pair and nodes c and d into another. This latter matching will reduce the sum of the shortest path lengths by at least 2 (p, q) units.

From the practical point of view, this observation has two effects: 1. It eliminates from consideration a very large percentage of the possible sets of matchings that might be considered. (This percentage might be expected to increase as the number of odd-degree nodes increases.) 2. It indicates that in a minimum-length matching odd-degree nodes will be matched to other odd-degree nodes in their immediate neighborhood.

Other observations (of a somewhat more complicated nature) have also been made (see [STRI 70]) with regard to finding good approximate solutions to minimum-length matching problems without using a matching algorithm. It has been the authors' experience that, whenever good maps of urban areas are available, it takes only a limited amount of practice with some examples before one develops the ability to find virtually by inspection excellent solutions to matching problems (by taking advantage of the foregoing observations).

Example 8

Consider again our initial Chinese Postman problem shown in Figure 6.12. The odd-degree nodes on Figure 6.12 are C, D, F, G, I, J, K, and L. They are shown on Figure 6.17, with that part of the network model of the district that contains all the shortest paths between the odd-degree nodes.

Inspection of Figure 6.17 leads to the conclusion that (although theoretically there are 7 · 5 · 3 · 1 = 105 possible sets of matchings among the eight odd-degree nodes) very few sets of matchings would even qualify for consideration. In fact, a couple of trials should be sufficient to convince the reader that the minimum-cost matching can only be the matching I-J, K-L, C-D, and F-G for a total cost (i.e., duplicated street length) of 490 units of length. The final result for the Chinese postman,s problem in this case is then shown on Figure 6.18, where edges to be traversed twice have been substituted by two edges (or pseudo-edges) each of equal length to the original one. The graph of Figure 6.18 now contains no nodes of odd degree, and thus an Euler tour can be drawn on it, beginning at any desired node and ending at the same node.

The length of all Euler tours on this graph will be equal to the total length of the original graph G (3,340 units) plus the distance to be traversed twice (490 units), for a total length of 3,830 units, or about 15 percent more than the total street length of the district that the mailman is responsible for. (This turns out to be the optimum solution.)