6.5.2 Median Problems
Let us consider an undirected network G(N, A) with n nodes. Let k be some
positive integer (k = 1, 2, 3, . . .) and let us choose k distinct points
on the graph G to be indicated as the set Xk = {xl,
x2, . . ., xk-1, xk}. We shall then
indicate by d(Xk,j) the minimum distance between any one of
the points x1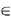 
Xk and the node j on G. That is,
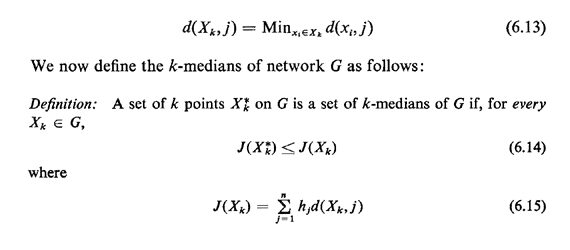
Now, if the k points in Xk are to be the points where k
facilities providing a given service will be located and if hj,
the demand weight of node j, is set equal to the fraction of all calls for
the service in question that originate from j
(i.e., 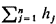 hj = 1), then finding the
k-medians, X*k , of G amounts to finding the set of
k locations that minimize the average travel distance to (or from) the
facilities by service users. This should be clear from the definition of
the function J(Xk) in (6.15), which is now nothing but an
expression for the average travel distance. Note, too, that the implicit
assumption in all of the above is that demands originating at any given
node j will be served exclusively by the facility that is
closest to j.
We can now state a most important result, known as Hakimi's
theorem [HAKI 64].
Theorem: At least one set of k-medians exist
solely on the nodes of G.
The practical significance of this theorem is great. It states in effect
that the search for the set of the k optimal locations for the k facilities
can be limited to the node set of G (i.e., to a total of n points only)
instead of the infinite number of points that lie on the links of G.
The validity of the theorem is obvious for the trivial case when the
required number of facilities k is greater than or equal to the number of
nodes n. Then we only have to locate one facility on each node to reduce
average travel distance to zero.
We shall now prove the theorem for the special case of a single facility
(k = 1). A line of approach similar to the one outlined below can be used
to prove the more general case (k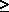 1) (see also Problem 6.9).
Proof (For a single facility, l-median): Suppose that the
optimum location for the single facility is at a point x which lies on the
link (p, q) between nodes p and q. The distance d(x, j) between x and any
vertex j 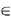N can then be written as
d(x, j) = Min (d(x, p) + d(p, j), d(x, q) + d(q,J)) (6.16)
That is, any node j 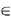N will be reached from x
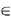(p, q) either through
p or through q. Let now P be the set of nodes that point x reaches most
efficiently through node p and Q the set of nodes reached more efficiently
through q (ties can be broken arbitrarily). P and Q are thus mutually
exclusive sets whose union is equal to N.
Assume now without loss of generality that more users are reached through
p than through q, that is
From the definition of the distance d(p, j), we have
But the term d(x, p) ·  is, by
assumption (6.17), greater than or equal to zero. Therefore, we conclude
that J(x) 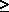J(p), which contradicts the assumption that the 1-median is
located at an interior point of the link (p, q). Stated differently, we have
proved that we can do "at least as well,, by moving the facility from x to
the node p. This also completes our proof.
Example 15: Location of a Single Medtan and of Two Medians
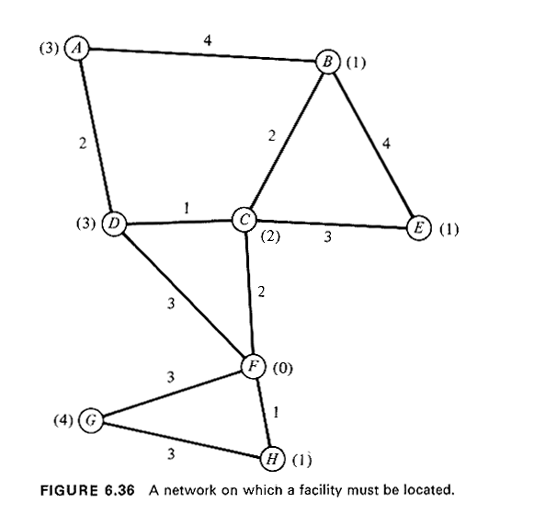
Consider the facility location problem of Figure 6.36, where a network
model of an urbanized area is shown. Nodes A through H represent points
where demands for service are generated and/or points where major roads in
the area intersect. A single facility is to be located in the area and its
prospective users will have to travel to the facility to partake of the
service provided there. Daily demand figures for the service (in units of
1OO's) are indicated by the figures in parentheses next to the nodes where
they originate. The lengths of the various road segments are also indicated
(in miles). Where should the facility be located to minimize the average
travel distance to it ?
Solution
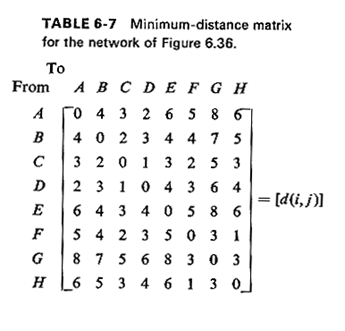
Because of Hakimi's theorem there are only eight candidate points on the
network for the placement of the facility; these are the eight nodes A
through H. By using Algorithm 6.2 (or some other shortest-path algorithm)
or, in this case by inspection, we can compute the distance (shortest-path)
matrix [d (i, j)] for all pairs of nodes, i and j, of the graph. The
distance matrix is given in Table 6-7.
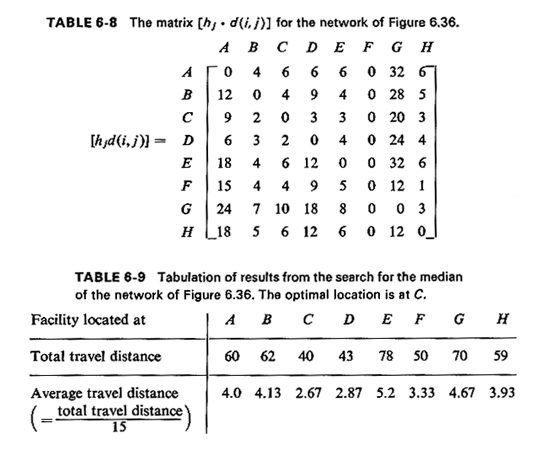
We next compute the terms hj · d(i, j) by multiplying each
column of the distance matrix by the weight of node j. The result of that
operation is shown in Table 6-8. Note that the entries of the
[hj · d(i, j)] matrix have very real physical meaning. For
instance, the entry of row B. column D, indicates that if the facility
is located at node B. users from node D must travel a total of 900
"passenger-miles" a day (= 300 persons x 3 miles) to use the facility at
B. In view of this, it should now be obvious how the optimum location
for the
facility can be found: by summing across the entries for each row i of
the [hj · d(i, j)] matrix, we can compute the total distance
traveled by users if the facility is located at row i. Normalizing the
quantities hj by dividing by the total demand (= 15), we can find
the average user travel distance associated with each of the eight candidate
locations. This procedure is summarized in Table 6-9. The optimum location
for the facility is at node C, and the associated average travel distance is
2.67 miles.
What would now happen if two facilities were desired? To solve the
2-median problem we can still take advantage of Hakimi's theorem and
consider only sets of points composed of two nodes. With a total of eight
nodes, there are (28) = 28 possibilities. Total (or
average) distances for each combination of locations can still be obtained
directly from the [hjd(i, j)] matrix of Table 6-8: demands from
each node will be "assigned" to the facility closest to it (i.e., the one
that requires the least amount of travel). Thus, if, for instance, the two
facilities are located at nodes A and G. the amount of travel contributed
by users from D is given by Min [hDd(A, D), hD ·
d(G, D)] = Min [6, 18] = 6, directly from the [hjd(i, j)]
matrix.
We list below the total distances associated with a few of the
28 combinations of locations:
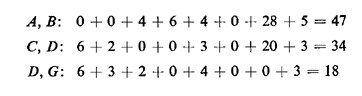
By exhaustive consideration of alI possibilities, we can reach the
conclusion that the solution of the 2-median problem consists of locations
at nodes D and G for a total distance of 18 units (or an average distance
of 1.2 miles). Under this solution, demand from nodes A, B. C, D, and E
(total of 10 units of demand) is assigned to the facility at D while demand
from G and H (total of 5 units) is assigned to G. Thus, the facility at D
assumes double the load of the facility at G. Note also that despite the
considerable overall reduction in the average travel distance, service
users from nodes B. C, and E now have to travel farther than they had to
with a single facility.
From the discussion above we immediately deduce an algorithm for
finding the one-median of an undirected graph G(N, A).
Single Median Algorithm (Algorithm 6.10)
| STEP 1: | Obtain the minimum distance matrix for the nodes of G.
| | STEP 2: | Multiply the jth column of the
minimum distance matrix by the demand weight hj
(j = 1, 2, . . ., n) to obtain the matrix hj · d(i j)].
| | STEP 3: | For each row i of the
[hj · d(i j)] matrix, compute the sum of all the terms in the
row. The node that corresponds to the row with the minimum sum of terms
is the location for the l-median.
|
Algorithm 6.10 can also be used, in principle, to obtain the k-medians
for any value of k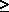
1. Only Step 3 must be modified to provide for
consideration of sets of k rows (rather than of single rows) in the manner
indicated for the 2-median case in our example.
Unfortunately, the combinations--and attendant required comparisons at
Step 3--become too many to handle even with a computer, as soon as the
number of nodes, n, and number of facility locations required, k, reach
moderate size. For instance, for n = 100 and k = 5 there exist some
75,000,000 possible combinations of 5-medians, with the computation of the
total distance for each requiring some 500 comparisons at Step 3.
Thus, the essentially "brute-force" approach of the modified Algorithm 6.10
soon becomes infeasible for k > 1 and more sophisticated approaches must be
sought.
Several exact algorithms have been proposed for the k-median problem
[REVE 70, GARF 74]. Basically, these algorithms attempt to solve efficiently
integer programming formulations of the problem. Better known is a
conceptually simple heuristic algorithm TEIT 68], which, however, does
not always terminate with the optimum k-median solution. We describe below
an improved version of that algorithm. It begins by finding the l-median
of the network and then increases the number of medians in steps of one at
a time, until they become equal to the required number, k (k > 1). Because
of Hakimi's theorem we shall only be concerned with locations on nodes.
We shall use S to indicate the set of nodes where medians have been
(tentatively) located at any given stage in the execution of the algorithm
and m to indicate the number of nodes in S. During the execution of the
algorithm m will increase from 1 to k.
Multimedian Heuristic Algorithm (Algorithm 6.11)
| STEP | 1 | Let
m = 1. Find the l-median of the network G(N, A) using Algorithm 6.10. Let
the l-median be at node i. Set S = {i}.
| | STEP | 2:
| (Facility Addition): Add a new facility to the current membership
of the set S by choosing that location among the nodes in ADS, the nodes
which are not in S.which produces the maximum possible improvement in the
objective function as the number of medians increases by 1. Let m = m + 1.
| | STEP | 3:
| (Solution Improvement): Attempt to improve the objective function
by substituting in a systematic way, one at a time, one of the nodes
in S with a node that is in N-S. Every time an improved solution is obtained,
use this as the new "incumbent" solution, S, and repeat Step 3. When all
possible single-node substitutions for a set S have been attempted without
improving the objective function, go to Step 4.
| | STEP | 4: | If m = k, stop; otherwise,
return to Step 2.
|
Example 15 (continued)
We now apply Algorithm 6.11 to the 2-median problem on the network of
Example 15. In Step 1 we find the 1-median at C and thus set S = {C}. In
Step 2, we must compare the value of the objective function for the sets of
facility locations {A, C}, {B. C}, {C, D}, {C, E}, {C, F}, {C, G}, and
{C, H}. Working with Table 6.8, the respective values of the objective
function are found to be 31, 38, 34, 37, 30, 20, and 29. Thus, 5 = {C, G}.
In Step 3, we now compare the incumbent solution successively with {A, Gl,
{s, G}, {D, G}. We obtain our first improvement with {D, G} (objective
function = 18). So S = {D, G} becomes the new incumbent solution and
Step 3 is repeated. We compare the new solution to {A, G}, {B. G},
{C, G}, {E, G}, . . . , {H. G}, {D, A}, {D, B}, . . . , {D, H} without
obtaining any further improvement in the objective function. (Note the
meaning of attempting "all possible singlenode substitutions.") Since,
in Step 4, m = 2 = k, the algorithm stops with the solution S = {D, G}.
In this case this also happens to be the optimum 2-median solution.
Algorithm 6.11 is typical of a number of heuristic network algorithms
that use the substitution method to improve initial solutions. For example,
one of the best-known algorithms for the traveling salesman problem
[LIN 73] begins with an initial tour and improves that tour by
substituting one link of the initial tour at a time with another link which
was not in the initial tour. The solutions obtained from such algorithms are
sometimes referred to as 1-optimal, because they cannot be improved by
replacing any single member (node, link, or whatever) of the final solution
set. Algorithm 6.11 could be easily modified to be 2-optimal (or 3-optimal,
etc.) by permitting the substitution in Step 3 of up to two
(or three, etc.) nodes of S at a time (instead of exactly one) with nodes
|
