6.5.5 Multiple CentersBy analogy to the k-medians problem, there is also a k-centers problem. The following definitions are appropriate. Let G(N, A) be an undirected network and let Xk =
{x1, x2, . . ., Xk} be a set of k points on
G. We shall use, as before, d(Xk, j) = Definition: A set of k points X*k on G is a
set of unconstrained (or absolute) k-centers of G. if for
every set Xk E G.
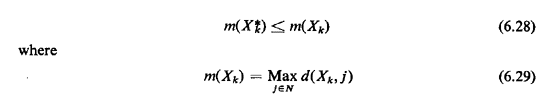
Definition: If the sets Xk, X*k in Definition 1 are constrained to consist solely of k nodes of the node set N. then the set X*k is a set of vertex k-centers of G. Until recently, k-center problems were believed to be among the most difficult graph problems to solve. The work of Handler [HAND 79] has, however, provided a set of algorithms--which he called "relaxation algorithms"--that solve efficiently problems of considerable size (e.g., n = 200, k= 5). |
d(xi, j) [i.e., d(Xk, j) is the minimum distance
between any one of the points xi 
Xk and the node j
on G].