7.2 Sample values of Gaussian random variables Let Z be a Rayleigh random varible (cf. Chapter 3, Example 3) with pdf



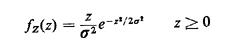
a. Show that a sample value, z, of A can be obtained by setting



where r, as usual, denotes a random number (0 r I).

In Chapter 3, Example 3, it was shown that if S and Tare independent Gaussian random variables with zero mean and standard deviation equal to that is, with pdf's



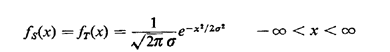
then the random variable Z = 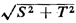has the Rayleigh Of shown above (the parameter 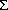is equal to the standard deviations of S and T).

b. Using this fact and the result of part (a), show that if X and Y are independent Gaussian random variables with mean mx and my, respectively, and equal standard deviations, 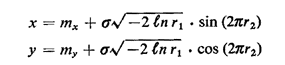then sample values, x and y, of X and Y can be obtained simultaneously by setting



where r1 and r2 are independent random numbers in the interval [0, 1]. This result has already been quoted [cf. expressions (7.13)-(7.15)].

Hint: Review carefully Example 3 of Chapter 3.