Unit Vectors as Directions

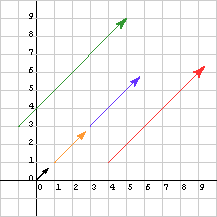
There can be infinitely many vectors in a given direction since the elements of a vector are real numbers. So, for example in two dimensions, there are an infinite number of vectors pointing along the x-axis. The column matrices for these vectors look like (s, 0)^T.

The unit vector for a given vector points in the same direction as that vector. There is only one unit vector in a given direction. There is only one value for the expression v/|v|. There is only one unit vector in the positive x direction, represented by ( +1, 0)^T.

The same is true for other orientations and other number of dimensions. The picture shows vectors of various lengths but same orientation. Only one of them is a unit vector.

Recall the formula:

angle   =   arc tan( y/x )

This formula is not very useful in three dimensions. When there are three axes it is not enough to determine the angle between a vector and just one axis.

Often the unit vector for a given vector is used to express the given vector's direction. There is only one such unit vector, so this description of direction is unique. This works for all dimensions.