The Answer Worked Out
In tedious detail:
- The two vectors are:
- p = ( -2, 4, 3)T
- q = ( 3, 1, -4)T
- The lengths are:
- |p|2 = ( -2, 4, 3)T · ( -2, 4, 3)T = 4 + 16 + 9 = 29
- |q|2 = ( 3, 1, -4)T · ( 3, 1, -4)T = 9 + 1 + 16 = 26
- The normalized vectors are:
- pu = (-2, 4, 3)T/
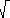 29
29 - qu = (3, 1, -4)T/
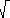 26
26
- pu = (-2, 4, 3)T/
- The dot product is:
- pu · qu = (-2, 4, 3)·(3, 1, -4)T/ (
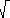 29
29 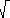 26)
26) - = (-6 + 4 - 12)/(
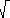 29
29 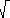 26)
= -14/(
26)
= -14/(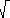 29
29 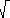 26) = -0.50985
26) = -0.50985
- pu · qu = (-2, 4, 3)·(3, 1, -4)T/ (
- The angle is:
- cos θ = -0.50985
- θ = arc cos( -0.50985) = 120.654°
Looks about correct.
