Visualizing the Cross Product
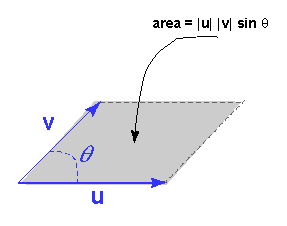
The picture shows two vectors u and v and the parallelogram they define between them.
The area of the parallelogram is: | u | | v | sin θ where θ is the enclosed angle.
This area is the same as the magnitude of the cross product. This fact is sometimes helpful in visualizing the cross product. For example, if u is rotated so that its orientation approaches that of v (but its length is not changed), the area of the parallelogram gets close to zero, as does the magnitude of the cross product.
