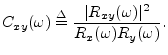
A function related to cross-correlation is the coherence function, defined in terms of power spectral densities and the cross-spectral density by
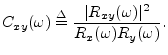
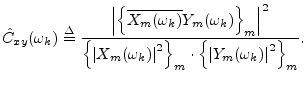
The coherence
![]() is a real function between zero and one
which gives a measure of correlation between
is a real function between zero and one
which gives a measure of correlation between ![]() and
and ![]() at
each frequency
at
each frequency ![]() . For example, imagine that
. For example, imagine that ![]() is produced
from
is produced
from ![]() via an LTI filtering operation:
via an LTI filtering operation:
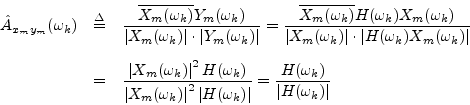
so that the coherence function becomes
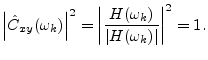
A common use for the coherence function is in the validation of
input/output data collected in an acoustics experiment for purposes of
system identification. For example, ![]() might be a known
signal which is input to an unknown system, such as a reverberant
room, say, and
might be a known
signal which is input to an unknown system, such as a reverberant
room, say, and ![]() is the recorded response of the room. Ideally,
the coherence should be
is the recorded response of the room. Ideally,
the coherence should be ![]() at all frequencies. However, if the
microphone is situated at a null in the room response for some
frequency, it may record mostly noise at that frequency. This is
indicated in the measured coherence by a significant dip below 1.
at all frequencies. However, if the
microphone is situated at a null in the room response for some
frequency, it may record mostly noise at that frequency. This is
indicated in the measured coherence by a significant dip below 1.