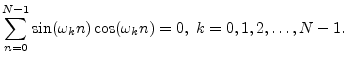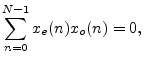Definition: A function
Some of the Fourier theorems can be succinctly expressed in terms of even and odd symmetries.
Definition: A function ![]() is said to be even if
is said to be even if
![]() .
.
An even function is also symmetric, but the term symmetric applies also to functions symmetric about a point other than 0.
Definition: A function ![]() is said to be odd
if
is said to be odd
if
![]() .
.
An odd function is also called antisymmetric.
Note that every finite odd function ![]() must satisfy
must satisfy
![]() .7.8 Moreover, for any
.7.8 Moreover, for any
![]() with
with
![]() even, we also have
even, we also have ![]() since
since
![]() ; that is,
; that is, ![]() and
and ![]() index
the same point when
index
the same point when ![]() is even.
is even.
Theorem: Every function ![]() can be decomposed into a sum of its even part
can be decomposed into a sum of its even part
![]() and odd part
and odd part ![]() , where
, where
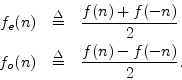
Proof: In the above definitions, ![]() is even and
is even and ![]() is odd by construction.
Summing, we have
is odd by construction.
Summing, we have
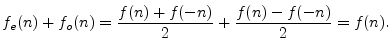
Theorem: The product of even functions is even, the product of odd functions
is even, and the product of an even times an odd function is odd.
Proof: Readily shown.
Since even times even is even, odd times odd is even, and even times odd is
odd, we can think of even as ![]() and odd as
and odd as ![]() :
:
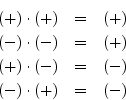
Example:
![]() ,
,
![]() , is an
even signal since
, is an
even signal since
![]() .
.
Example:
![]() is an odd signal since
is an odd signal since
![]() .
.
Example:
![]() is odd (even times odd).
is odd (even times odd).
Example:
![]() is even (odd times odd).
is even (odd times odd).
Theorem: The sum of all the samples of an odd signal ![]() in
in ![]() is zero.
is zero.
Proof: This is readily shown by writing the sum as
![]() , where the last term only occurs when
, where the last term only occurs when ![]() is even. Each
term so written is zero for an odd signal
is even. Each
term so written is zero for an odd signal ![]() .
.
Example: For all DFT sinusoidal frequencies
![]() ,
,