A key property of sinusoids is that they are orthogonal at different frequencies. That is,
For length ![]() sampled sinusoidal signal segments, such as used
by the DFT, exact orthogonality holds only for the harmonics of
the sampling-rate-divided-by-
sampled sinusoidal signal segments, such as used
by the DFT, exact orthogonality holds only for the harmonics of
the sampling-rate-divided-by-![]() , i.e., only for the frequencies
, i.e., only for the frequencies
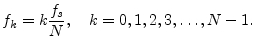
The complex sinusoids corresponding to the frequencies ![]() are
are