Response areas were not optimized in any sense, such as was done
for N = 2 in Section 5.3.4.
The removal of the equal-service-times assumption poses few problems.
Instead of the downward transition rates on the hypercube all being
equal, they would in general be different, with a downward rate for
server n being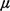 
n (where
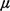n-1 would be the
mean service time of server n). Minor complications arise in
computing system performance measures, particularly for the case of
queued requests, and these are discussed in Problem 5.13.
The queue capacity of the hypercube model can, in general, assume any
value from 0 to infinity. In fact, Problem 5.7 asks you to develop
results analogous to (5.31)-(5.44) for the zero-capacity situation. The
restriction on the options available for queue depletion remains an
obstacle to obtaining more realistic geographically-based queue
disciplines.
The upward transition rates on the hypercube model need not represent
simple fixed preference dispatching with no ties. Allowing ties is
relatively straightforward, as demonstrated in the publicly available
version of the hypercube model [LARS 75b]. Of greater interest is the
generalization to non-fixed-preference dispatching. The major problem
encountered with state-dependent policies occurs with large N in
the computation of the system performance measures and even in the
initial determination of the upward transition rates [JARV 75].
Recently, the mathematics have been worked out (for efficient computer
solution) for a dispatch policy that always dispatches the real-time
closest unit, even if some or all of the units are non-fixed-position
units [LARS 78]. This policy models a dispatcher utilizing an AVL
(automatic vehicle locator) system. We ask you to develop such a model
in an analytically tractable N = 3 setting in Problem 5.8.
The generalization of the Carter-Chaiken-Ignall optimization
procedure (for optimal design of response areas) has been worked out for
arbitrary N by Jarvis. The procedure is algorithmic; that is, the
end result is a set of optimal response areas for a particular set of
model parameters. Jarvis finds the same insensitivity of mean travel
time to shifts from equal travel time boundaries to optimal
state-dependent boundaries. However, the utility of the method for
balancing server workloads is still high [JARV 75].
In implementing the basic model of this section (or any of its
generalizations) on a computer, one immediately confronts substantial
problems of computer storage and execution time. For an N = 10
problem, there are 210 = 1,024 states, and thus 1,024
simultaneous linear equations must be solved to obtain the hypercube
state probabilities. The addition of one server doubles the size
of the problem to 211 = 2,048 equations. For N = 15,
215 32,768 and the problem quickly gets out of hand, even for
today's very large computers. For instance, just to store the
state-transition matrix (if we did not take advantage of its special
properties such as sparcity) would require 215 X
215 = 230 = 1,073,741,824 elements of storage.
Thus, as discussed in [LARS 74a], much time has been invested in using
the special structure of the hypercube model to derive
computer-efficient means for developing and solving its equations. We
expect to see more work in this direction in the future, that is, the
use of queueing theory to develop large sets of simultaneous equations
which have a special structure that can be exploited for efficient
computer solution. Much work in queueing networks has already had this
flavor [KLE1 75, 76; FRAN 71].
