Length is always Positive

Since the square of length is a sum of squares, and squares (of real numbers) are always positive, length must always be positive.

| a |  =  | (a1, a2,  a3 )T | 
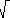      =  ( a12 + a22 + a32 )
      >=    0

The only time the length of a 3D vector is zero is when the vector is the zero vector. In all coordinate frames the 3D zero vector is represented by:

0 =  ( 0, 0, 0)T

So its length is:

| 0 |  =   ( 02 + 02 +  02 )
      =   0

Of course, the length of the 2D zero vector is also zero, and it is the only 2D vector with zero length.