Radians
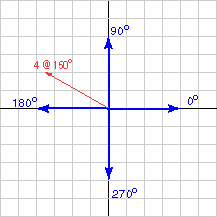
The steps in this calculation are:
- Draw a sketch: see diagram
- Calculate x by projecting the length onto the x-axis:
4 * cos( 150 ) = -3.464 - Calculate y by projecting the length onto the y-axis:
4 * sin( 150 ) = 2.0 - Check answers against the sketch: Looks OK.
Be cautious about plugging into these formulae and expecting correct answers, especially when programming in C or Java. Math libraries for a programming language can do unexpected things if you are not careful.
There are three places to be especially cautious:
- The argument for sin(), cos(), tan() is expected in radians. The return value of atan() is in radians.
- The argument for most math functions is expected to be a double. In "C", if you supply a float or an int, you won't get a error message, just a horribly incorrect answer.
- There are several versions of "arc tan" in most C libraries, each for a different range of output vaues.
Now would be a good time think about radians. Usually in professional circles, angles are expressed in radians. Angles are measured counterclockwise from the positive x axis (or sometimes a negative angle is measured clockwise from the positive x axis.
There are 2 pi radians per full circle. Or 2 pi radians = 360o
