Direction of a Unit Vector
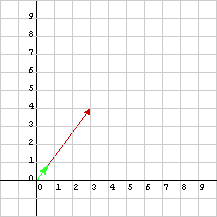
Scaling changes the length of a vector but not its direction. If vu is the unit vector corresponding to v, then vu and v have the same orientation.
This sounds plausible, but a demonstration might not hurt:
Start with v = (3, 4)T as above.
Form vu = (3/5, 4/5)T.
The direction of v is arc tan( 4/3 ).
The direction of vu is
arc tan( (4/5) / (3/5) ) =
arc tan( (4/5) * (5/3) ) =
arc tan( 4/3 ).
