Scaling
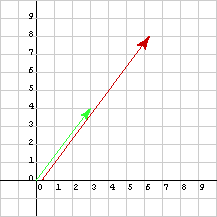
Does the guess work?
- (New length)2 = 62 + 82 =
2232 + 2242 =
22(32+42) = 22(old length)2 - So, taking roots, (New length) = 2(old length)
- By similar triangles, the direction is the same.
Or you could notice: new direction = arc tan( 8/6 ) = arc tan( 4/3 ) = old direction. It looks like the guess worked.
In talking about vectors, a real number is sometimes called a scalar.
Scaling a geometrical vector means keeping its orientation the same but changing its length by a scale factor. It is like changing the scale of a picture; the distances expand or shrink, but the directions remain the same.
If a vector is represented by a column matrix (x, y)T then scaling by the a number multiplies each element:
a(x, y)T = (ax, ay)T
This works for 3 dimensional vectors also:
If v is represented by
