The Dot Product
|
|
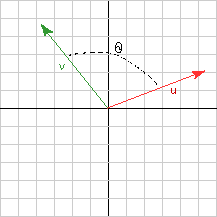
For geometrical vectors in two or three dimensional space, the dot product of two vectors u and v is:
u · v = |u| |v| cos θ
The dot product is indicated by the dot between the two vectors. Unfortunately, many browsers do not show the dot very clearly. You may see a very tiny dot, or a small black bar. θ is the angle between the two vectors.
Don't write two vectors next to each other like this: uv when you want the dot product. Always put a dot between them: u · v .
In 2D the two vectors lie in a plane (of course) and the angle between them is easy to visualize.
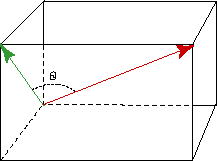
In 3D two vectors also lie in a plane embedded within the 3D space, except when the two vectors are co-linear (when they both point in the same direction).
When two vectors are co-linear, the angle between them is zero and so:
u · v = |u||v| cos 0 = |u||v| 1 = |u||v|
