A good answer might be:
What is the cosine of the angle between these unit vectors:
- s = (1, 0, 1)T/
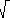 2
2 - t = (1, 1, 1)T/
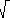 3
3 - cos θ
= (1, 0, 1)T · (1, 1, 1)T / (
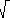 2
2 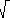 3)
= 2/(
3)
= 2/(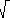 2
2 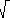 3)
=
3)
= 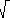 2 /
2 / 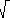 3
= 0.8164
3
= 0.8164
What is the cosine of the angle between these unit vectors:
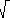 2
2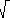 3
3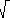 2
2 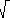 3)
= 2/(
3)
= 2/(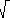 2
2 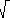 3)
=
3)
= 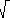 2 /
2 / 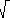 3
= 0.8164
3
= 0.8164The dot product formula can be used to work out some geometric problems that otherwise would be hard. In the following figure, the red edges of the figure coincide with the coordinate axes. They share a mutual endpoint at (0, 0, 0). The edge along the x axis ends at x=2; the edge along the y axis ends at y=3; and the edge along the z axis ends at z=4. The remaining edges connect these endpoints.
Now say that you wanted to calculate the angle between the two green edges. This might be fairly tedious using trigonometry. But now you can: