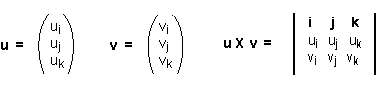Memory Aid
Here is a way to compute the cross product by arranging the elements of each vector into a determinant. The top row contains the symbols that stand for each axes. This is not the definition of cross product. In fact, it is not even a determinant. It is merely a memory aid.
This only works for three dimensional vectors (the cross product is not defined for vectors of any but three dimensions). Put the first vector's components into the second row, and the second vector's components into the third row.