Not Associative

Fussing with math gives the same result:

| (ku) × v |   =   | ku | | v | sin θ   =   | k | |u | | v | sin θ

The magnitude is | k | times the magnitude of u × v. And the orientation of the result must be the same. So the answer is correct.

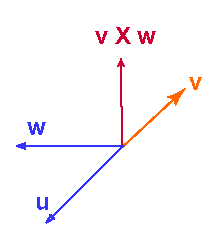
Another fact is that, in general,   (u × v) × w  =/=  u × (v × w)

To see this, look at the diagram and mentally form the cross product (u × v) , then take the cross product of that with w. Then form the cross product (v × w) and take the cross procut of u with that.