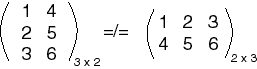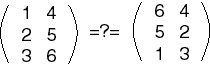Matrix Equality
For two matrices to be equal, they must have
- The same dimensions.
- Corresponding elements must be equal.
In other words, say that
Then A = B if and only if n=p, m=q, and aij=bij for all i and j in range.
Here are two matrices which are not equal even though they have the same elements.