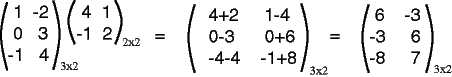Dimensions of the Result
If two rectangular matrices are put in order so that the inner dimension is the same in each, then the matrices are conformant and can be multiplied. The result is (in general) a rectangular matrix:
AR×N BN×C = DR×C
Look at the dimensions in the following product (for now, ignore how the elements were calculated):
The the product AB (if it can be formed) has the same number of rows as A and the same number of columns as B. You can think of this as "canceling" the inner dimension.