Constant Multiplier

Features

• Parameterized word lengths and constant values

• Unsigned and signed (Two’s-Complement) data representation

• Booth / Wallace architecture

• Behavioral simulation model (for non-pipelined multiplier only) in VHDL and Verilog

Family Support

SX, SX-A, eX, 500K, PA, Axcelerator, ProASIC3/E, Fusion

Description

The Constant Multiplier performs the multiplication of a data-input with a constant value. Area and performance of the Constant Multiplier depend on the value of the constant. Specifically, area and performance depend on the number of groups of 1s in the bit pattern of the constant. As a result, the worst-case constant has a bit pattern of alternating 1s and 0s (…010101…). However, even for that worst-case the area and performance of the Constant Multiplier is superior to a regular Multiplier.

The Constant Multiplier core output wordlength is always double the input wordlength. Depending on the value of the constant, some of the most significant bits might be sign-extension bits. You may be able to reduce hardware by calculating the actual number of bits needed and cutting all sign-extension bits. For example:

width =4, Constant = 1100, representation=signed

The worst case data for this example would be 1000 (-8) and therefore the worst case output data would be 010 0000 (-8 * -4 = 32). So with that we know that Mult<8> is just a sign-extension bit (Mult<8> = Mult<7>).

Keep in mind that some constant multiplications might be generated even more effectively, e.g. constants to the power of 2 are just shift-operations, or constants like 3,5,7,9,10, etc. can be generated using shift operations and a simple addition/subtraction (2+1, 4+1, 8-1, 8+1, 8+2, etc.) For these constants, the implementation of the Constant Multiplier might not be as efficient as using shift operations and/or Adders/Subtractors.

Usually synthesis infers regular Multipliers even for constant values. Therefore the use of the Constant Multiplier core in a design, which performs one or more multiplications with constant values, is expected to be very beneficial.

An application example might be FIR-filters with constant coefficients, where the computation is organized in the “transposed form” as indicated in the figure below.

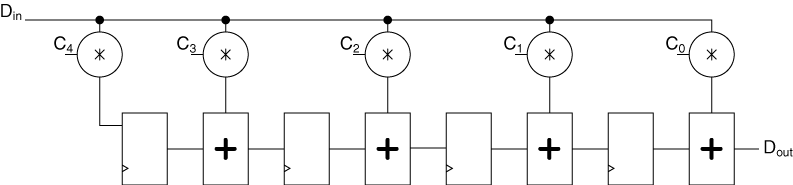
FIR-Filter Organized in the "Transposed Form" Using Constant Multipliers

Parameter Rules:

1. DataA is always binary and of the size of Width.

2. Constant must be of the selected Radix and be of the selected width for HEX/BIN. SmartGen automatically pads zeroes if they are missing.

e.g.: Radix: BIN, Width: 5, Constant: 00010
Radix Hex, Width:8, Constant: 0A