네이버

http://blog.naver.com/PostPrint.nhn?blogId=babojay&logNo=40039111521#

Chapter 6.
Dataflow Modeling

 

 - 작은 회로의 경우는 gate의 수가 제한적이며 하나 하나 gate instantiation을 하고 연결을 할 수 있기 때문에 Gete-level modeling으로도 충분하다. 더구나 기초적인 디지털 회로 지식만 있다면 설계방법이 매우 직관적일 수 있다. 하지만 회로가 복잡해지고 gate수가 늘어나면서 더 효율적인 설계 방법이 필요하였다. Dataflow modeling은 레지스터간 데이터의 이동과 그 데이터의 처리에 관하여 기술하는 설계 방법이다. 요즘엔 Logic synthesizer의 발전으로 Dataflow modeling을 자동으로 Gate-level modeling으로 변환해 주면서 Dataflow Modeling이 더욱 각광을 받고 있다. 설계과정의 유연함을 극대화하기 위하여 Gate-level, Dataflow, Behavioral 설계개념을 아우르는 Verilog Description이 대세이며, Dataflow와 Behavioral의 조합인 RTL(Register Tansfer Level)설계 방법이 일반화되었다.

 

*Objectives
 - assign(continuos assignment)구문 , assign 구문의 제한, Implicit assignment 구문
 - Assignment delay, Implicit assignment delay, Net declaration delay
 - Expressions, Operators, Operands
 - Operator types - 수학, 논리, 관계, 등가, bitwise, reduction, shift, concatenation,

                           conditional
 
6.1 Continuous Assignments
 
 - Dataflow modeling에서 가장 기본적인 구문이다.
 - Continuous란 연속적이다. 끊김이 없다라는 뜻이다. H/W에서는 어떤 의미일까? 시간에 대한 연속일 것이다. 다시 말하면 assigning 중에 저장하는 과정이 없다는 말이다. register나 latch의 기능이 없는 digital 회로 개념에서는 조합회로(combinational)이라고 하면 비슷할 것이다.
 
 Syntax]

    <continuous_assign>
        ::= assign <drive_strength>?<delay>? <list_of_assignment>;

 

 - <drive_strength>?, <delay>? 는 option이다.
 - drive_strength는 strength level로 지정해 줄 수 있으며 기본값은 strong1, strong0이다.
 - delay는 시간단위로 지정해줄 수 있다.

 

 continuous assginment의 특징을 정리하면 다음과 같다.
    1. assign의 왼쪽에 올 수 있는 것은 net이다. register는 올 수 없다.
    2. delay를 포함하여 오른쪽의 변화가 결정되어짐과 동시에 assign된다.
    3. 오른쪽에는 net, register, function call등이 올 수 있다.
    4. Delay를 지정해 줄 수 있으며, 이는 gate delay를 정하는 것과 유사하다.

Ex)
    // out, i1, i2 는 모두 net
    assign out = i1 & i2;

 

    // addr는 16-bit vectorr net, addr1과 addr2는 16-bit register
    assign addr[15:0] = addr1[15:0] ^ addr2[15:0];

 

    // Concatenation. c_out과 sum[3:0]이 합쳐져 5-bit net으로 간주된다.
    assign {c_out, sum[3:0]} = a[3:0] + b[3:0] + c_in;

 

6.1.1 Implicit Continuous Assignment

 - 다음의 예처럼 net을 선언하면서 암묵적으로 assign이 이루어지기도 한다.

Ex)
    // 보통의 예
    wire out;
    assign out = in1 & in2;

 

    // Implicit Assign
    wire out = in1 & in2;

 

6.2 Delays

6.2.1 Regular Assignment Delay
 - assign 키워드 뒤에 time unit으로 명시해준다.
 - 오른쪽의 operand의 변화가 생길때 delay만큼의 시간후에 수식을 재계산하여 결과에 반영하게 된다.

Ex)
    assign #10 out = in1 & in2;

 

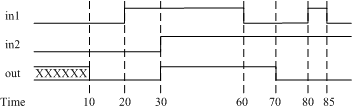
그림 6.1 Delays

 

 - 20 에서 in1과 in2가 'H'로 올라가고 그 결과가 10뒤인 30에 나타난다.
 - 마찬가지로 60에 in1이 'L'로 내려오고 그 결과가 70에 나타난다.
 - 80에 in1이 'H'로 올라갔으나 delay time 10이 흐른 90에 결과를 재계산하게 돤다. 하지만 delay time이 10이 되기 전에 'L'로 내려갔기 때문에 90에서 재계산 결과는 'L'이 된다.
 - 이런 이유로 inertial delay(관성 딜레이)라고도 한다.

 

6.2.2 Implicit Continuous Assignment Delay

 

Ex)
    // Implicit delay
    wire #10 out = in1 & in2;

 

6.2.3 Net Declaration Delay

 - Net를 선언할 때 그 net에 delay를 지정할 수 있다.

Ex)
    // Net Delay
    wire #10 out;
    assign out = in1 & in2;

 

6.3 Expressions, Operators and Operands

6.3.1 Expressions
 - 피연산자와 연산자로 이루어져 결과를 갖는 일종의 수식.

Ex)
    // Expressions
    a ^ b
    addr1[20:17] + addr2[20:17]
    in1 | in2

 

6.3.2 Operands
 - Constant, integer, real number, net, register, times, bit-select, part-select등 거의 모든 data type과 memory, function call도 가능하다.

Ex)
    // Operands
    integer count, final_count
    final_count = count + 1;    // count : integer operand, 1 : constant operand

 

    real a, b, c;
    c = a - b;         // a, b : real operand

 

    reg [15:0] reg1, reg2;
    reg [3:0] reg_out;
    reg_out = reg1[3:0] ^ reg2[3:0]; // reg1[3:0], reg2[3:0]: part-select operand

 

    reg ret_value;
    ret_value = calculate_parity(A, B);    // function call(calculate_parity) operand

 

6.4 Operator Types

 

 

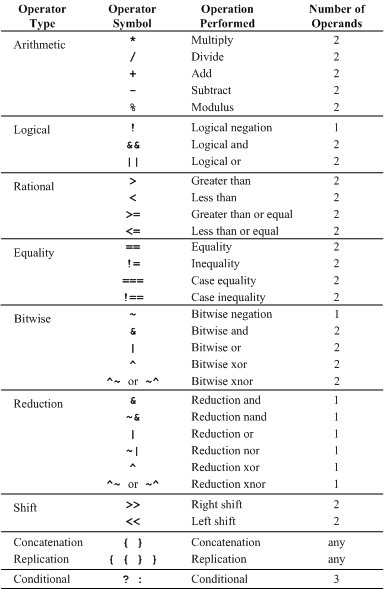
표 6.1 Operator types

 

6.4.1 Arithmetic Operators
 - Binary operator : 2개의 operand를 가지는 operator
Ex)
    A * B     // 곱하기.
    D / E     // 나누기
    A + B    // 더하기
    B - A     // 빼기.
    D % E   // 나머지. (modulus)

 

    in1 = 4'b101x; in2 = 4'b1010;
    sum = in1 + in2;     // sum : 4'bx

 

   13 % 3    // modulus operator(나머지) 결과는 1
   -7 % 2     // -1
    7 % 2     // 1

 

 - Unary operator : operand앞에 붙는 +, -

Ex)
    -4       // negative 4
    +5      // positive 5

 

    -10 / 5       // 결과는 -2
    -'d10 / 5    // 결과는 정확하지 않으며 예측할 수 없게 된다.
                     // -'d10 -> 2'comp of 10 -> 2^32 - 10

 

6.4.2 Logical Operators
 - and(&&), or(||), not(!):  &&, || 는 binary, ! 는 unary이다.
 - 연산의 결과는 항상 1-bit의 true(1), false(0), x 로 나타난다.
 - 연산의 결과가 0 이면 false, 0이 아니면 true가 되지만, operand중 어느하나라도 x나 z를 갖고 있다면 결과는 x가 된다.
 
Ex)
    // Logical operation
    A = 3; B = 0;

    A && B    // (true AND false)의 관계이므로 결과는 false(0)이다.
    A || B      // (true OR false)의 관계이므로 결과는 true(1)이다.
    !A           // NOT(true)이므로 결과는 false(0)이다.
    !B           // NOT(false)이므로 결과는 true(1)이다.

 

    A = 2'b0x; B = 2"b10;
    A && B       // (x AND true)이므로 결과는 x

 

    (a == 2) && (b == 3)   // a=2, b=3인 경우에만 true(1), 그 이외는 false(0)

 

6.4.3 Relation operator
 - 크고( >) 작고(<) 크거나 같고(>=) 작거나 같고(<=)의 관계를 구한다. Operand중에 x나z가 존재하면 그 수식의 결과는 x가 된다.

Ex)
    // A = 4, B = 3
    // S = 4'b1010, T = 4'b1101, U = 4'b1xxx

 

    A <= B      // 결과는 0
    A > B        // 결과는 1
    T >= S      // 결과는 1
    T < U        // 결과는 x

 

6.4.4 Equality Operator
 - Logical equality(==, !=)와 case equality(===, !==)의 두가지가 존재한다.
 - Logical equality는 논리 연산의 결과를 따진다. 즉, operand에 x, z가 존재하면 결과는 x가 된다.
 - Case equality는 논리 연산과는 무관하게 operand가 무슨 값이든 일대일로 동일한지의 여부만 따진다.

Ex)
    // A = 4, B = 3
    // J = 4'b1010, K = 4'b1101
    // S = 4'b1xxz, T = 4'b1xxz, U = 4'b1xxx

 

    A == B      // false
    J != K        // true
    J == S       // x(unknown)
    S === T    // true
    T !== U     // true

 

6.4.5 Bitwise Operators
 - bit단위의 논리 연산이다.
 - operand의 bit수가 다른 경우 작은 bit수의 MSB쪽으로 0이 채워 큰 쪽과 같게 만든다.
 - 연산의 결과는 bit에만 한정되며 다른 bit에 영향을 주지 않는다.

Ex)
    //  A = 4'b1010, B = 4'b1101, C = 4'b10x1

 

    ~A          // 4'b0101
    A & B      // 4'b1000
    A | B       // 4'b1111
    A ^ B      // 4'b0111
    A ^~ B    // 4'b1000
    A & C      // 4'b10x0

 

6.4.6 Reduction Operators

 - 하나의 operand내의 bit들과의 논리연산으로 결과는 1-bit이다.
 - &, ~&, |, ~|, ^, ~^(^~) 등binary operator이지만 사용법은 unary operator이다.

Ex)
    // A = 4'b1010

 

    &A     // 1 & 0 & 1 & 0  -> 1'b0
    |A      // 1 | 0 | 1 | 0  -> 1'b1
    ^A     // 1 ^ 0 ^ 1 ^ 0  -> 1'b0

 

6.4.7 Shift Operators

 - 오른쪽이나 왼쪽으로 명시한 만큼 bit를 옮기는 연산자
 - 옮기면서 생기는 빈 자리는 0으로 채워진다.

Ex)
    // A = 4'b1100

 

    Y = A >> 1;    // 4'b0110
    Y = A << 1;    // 4'b1000
    Y = A << 2;    // 4'b0000

 

6.4.8 Concatenation Operator
 - size가 명시된 operand만 사용 가능하다.
 - net, reg, vector, bit-select, part-select, sized constant등을 하나로 연결하는 연산자 ( {, } )

Ex)
    // A = 1'b1, B = 2'b00, C = 2'b10, D = 3'b110

 

    Y = {B, C};                         // Y = 4'b0010
    Y = {A, B, C, D, 3'b001};    // Y = 11'b1_00_10_110_001
    Y = {A, B[0], C[1]};            // Y = 3'b101

 

6.4.9 Replication Operator
 - Concatenation의 operand를 몇 번 반복해서 넣을 것인가 지정하는 연산자

Ex)
    reg A;
    reg [1:0] B, C;
    reg [2:0] D;

 

    A = 1'b1; B = 2'b00: C = 2'b10; D = 3'b110;

 

    Y = { 4{A} };                   // Y = 4'b1111
    Y = { 4{A}, 2{B} };         // Y = 8'b11110000
    Y = { 4{A}, 2{B}, C };     // Y = 11'b11110000110

 

6.4.10 Conditional Operator

 - Condition_expr ? true_expr : false_expr;
 - Condition_expr를 면저 계산하고 그 결과가 true이면 true_expr가 실행되고, false이면 false_expr가 실행된다.
 - Condition_expr가 x일 경우, true_expr, false_expr모두 계산하여 결과를 bit단위로 비교한다. 같으면 그 값으로, 다르면 x로 결정된다.
 - true_expr, false_expr는 각각 conditional operation이 들어갈 수 있다. 즉 nesting이 허용된다.

Ex)
    // modeling tristate buffer
    assign addr_bus = drive_enable ? addr_out : 36'bz;

 

    // modeling 2-to-1 mux
    assign out = control ? in1 : in0;

 

    // nesting
    assign out = (A == 3) ? (control ? x : y) : (control ? m : n);

 

6.4.11 Operator Precedence

 - 각 연산자들의 우선순위는 다음과 같다.
 - 코드를 읽기 쉽게 하기 위해 괄호를 적절히 사용하여 주는 것이 좋다.

 

표 6.2 Operator Precedence

6.4 Examples

 - 전에 다루었던 4-to-1 multiplexer와 4-bit full adder를 dataflow를 이용하여 modeling하여 본다.

 

6.5.1 4-to-1 Multiplexer

 - Method 1: Logic Equation

Ex)
    // 4-to-1 Multiplexer with Dataflow, Logic Equation
    module mux4_to_1 (out, i0, i1, i2, i3, s1, s0);

 

    output out;
    input i0, i1, i2, i3;
    input s1, s0;

 

    // Logic equation for out
    assign out = (~s1 & ~s0 & i0) |
                      (~s1 & s0 & i1) |
                      (s1 & ~s0 & i2) |
                      (s1 & s0 & i3);
   
    endmodule

 

 - Method 2: Conditional Operator

Ex)
    // 4-to-1 Multiplexer with Dataflow, Conditional Operator
    module mux4to1( out, i0, i1, i2, i3, s1, s0);

 

    output out;
    input i0, i1, i2, i3;
    input s1, s0;
   
    // Nested conditional operator
    assign out = s1 ? (s0 ? i3 : i2) : (s0 ? i1 : i0);

    endmodule

 

 - 참고로 Chapter 5에서 gate-level로 modeling 했던 예제를 비교해본다.

Ex)
    // 4-to-1 MUX in Gate-level description
    module mux4_to_1(out, i0, i1, i2, i3, s1, s0);

 

    output out;                       // Port declaration
    input i0, i1, i2, i3;
    input s1, s0;

 

    wire s1n, s0n;                 // Internal wire
    wire y0, y1, y2, y3;

 

    not (s1n, s1);                 // create s1n, s0n
    not (s0n, s0);

 

    and (y0, i0, s1n, s0n);     // 3-input and gate
    and (y1, i1, s1n, s0);
    and (y2, i2, s1, s0n);
    and (y3, i3, s1, s0);

 

    or (out, y0, y1, y2, y3);    // 4-input or gate

 

    endmodule

 

6.5.2 4-bit Full Adder

 - Method 1: Dataflow Operator

Ex)
    // 4-bit Full Adder with dataflow statement
    module fulladd4 (sum, c_out, a, b, c_in);

 

    output [3:0] sum;
    output c_out;
    input [3:0] a, b;
    input c_in;

 

    assign {c_out, sum} = a + b + c_in;

 

    endmodule

 

 - Method 2: full addder with carry lookahead

Ex)
    module fulladd4 (sum, c_out, a, b, c_in);

 

    output [3:0] sum;
    output c_out;
    input [3:0] a, b;
    input c_in;

 

    wire p0, g0, p1, g1, p2, g2, p3, g3;
    wire c4, c3, c2, c1;

 

    assign p0 = a[0] ^ b[0],
              p1 = a[1] ^ b[1],
              p2 = a[2] ^ b[2],
              p3 = a[3] ^ b[3];

 

    assign g0 = a[0] & b[0],
              g1 = a[1] & b[1],
              g2 = a[2] & b[2],
              g3 = a[3] & b[3];

 

    assign c1 = g0 | (p0 & c_in),
              c2 = g1 | (p1 & g0) | (p1 & p0 & c_in),
              c3 = g2 | (p2 & g1) | (p2 & p1 & g0) | (p2 & p1 & p2 & c_in),
              c4 = g3 | (p3 & g2) | (P2 & p2 & g1) | (p3 & p2 & p1 & g0) |

                                                                       (p3 & p2 & p1 & p0 & c_in);

    assign sum[0] = p0 ^ c_in,
              sum[1] = p1 ^ c1,
              sum[2] = p2 ^ c2,
              sum[3] = p3 ^ c3;

 

    assign c_out = c4;

 

    endmodule

 

   * 4 단계의 gate를 거치면서 propagation delay가 일정하게 된다.
  ** logic 은 복잡해지지만 bit수가 늘어나더라도 propagation delay는 늘어나지 않는다.

 

6.5.3 Ripple Counter

 - 전에 다루었던 4-bit ripple counter를 dataflow의 구문으로 modeling 해본다.

 

 

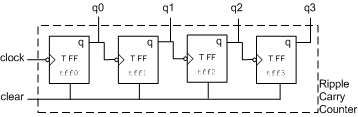
그림 6.2 4-bit Ripple Carry Counter

 

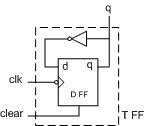
그림 6.3 T-flipflop

 

 

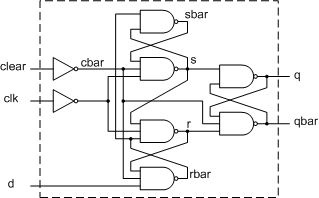
그림 6.4 Negative Edge Triggered D-F/F

 

Ex)
    // 4-bit Ripple Counter
    module counter (Q, clock, clear);

 

    output [3:0] q;
    input clock, clear;

 

    T_FF tff0 (q[0], clock, clear);
    T_FF tff1 (q[1], q[0], clear);
    T_FF tff2 (q[2], q[1], clear);
    T_FF tff3 (q[3], q[2], clear);

 

    endmodule

 

    // Edge-triggered T-F/F
    module T_FF (q, clk, clear);

 

    output q;
    input clk, clear;

 

    edge_dff ff1(q, , ~q, clk, clear);      // instantiation of edge_dff
                                                          // complement of q is fed back to d
                                                          // qbar is not connected

    endmodule

 

    // Edge-triggered D-F/F
    module edge_dff (q, qbar, d, clk, clear);

 

    output q, qbar;
    input d, clk, clear;

 

    wire s, sbar, r, rbar, cbar;

 

    assign cbar = ~clear;
 
    assign sbar = ~(rbar & s),
              s = ~(sbar & cbar & ~clk),
              r = ~(rbar & ~clk, s),
              rbar = ~(r & cbar & d);

 

    assign q = ~(s & qbar),
              qbar = ~(q & r & cbar);

 

    endmodule

 

 - Stimulus block

Ex)
    // Top level stimulus module
    module stimulus;

 

    reg CLOCK, CLEAR;
    wire [3:0] Q;

 

    initial
        $monitor($time, " Count Q = %b, Clear = %b", Q[3:0], CLEAR);

 

    counter c1(Q, CLOCK, CLEAR);

 

    initial
    begin
        CLEAR = 1'b1;
        #34 CLEAR = 1b0;
        #200 CLEAR = 1'b1;
        #50 CLEAR = 1'b0;
    end

 

    initial
    begin
        CLOCK = 1'b0;
        forever #10 CLOCK = ~CLOCK;
    end

 

    initial
    begin
        #400 $finish;
    end

 

    endmodule

 

 - 시뮬레이션 결과

            0 Count Q = 0000, Clear = 1
          34 Count Q = 0000, Clear = 0
          40 Count Q = 0001, Clear = 0
          60 Count Q = 0010, Clear = 0
          80 Count Q = 0011, Clear = 0
        100 Count Q = 0100, Clear = 0
        120 Count Q = 0101, Clear = 0
        140 Count Q = 0110, Clear = 0
        160 Count Q = 0111, Clear = 0
        180 Count Q = 1000, Clear = 0
        200 Count Q = 1001, Clear = 0
        220 Count Q = 1010, Clear = 0
        234 Count Q = 0000, Clear = 1
        284 Count Q = 0000, Clear = 0
        300 Count Q = 0001, Clear = 0
        320 Count Q = 0010, Clear = 0
        340 Count Q = 0011, Clear = 0
        360 Count Q = 0100, Clear = 0
        380 Count Q = 0101, Clear = 0