In the preceding section we saw that the running time of DequeueHead is O(1), but that the running time of DequeueTail is O(n), for the pointer based implementation of a deque. This is because the linked list data structure used, LinkedList<T> is a singly-linked list . Each element in a singly-linked list contains a single pointer--a pointer to the successor (next) element of the list. As a result, deleting the head of the linked list is easy: The new head is the successor of the old head.
However, deleting the tail of a linked list is not so easy: The new tail is the predecessor of the original tail. Since there is no pointer from the original tail to its predecessor, the predecessor must be found by traversing the linked list from the head. This traversal gives rise to the O(n) running time.
In a doubly-linked list ,
each list element contains two pointers--one to its successor and one to its predecessor.
There are many different variations of doubly-linked lists:
Figure ![]() illustrates four of them.
illustrates four of them.
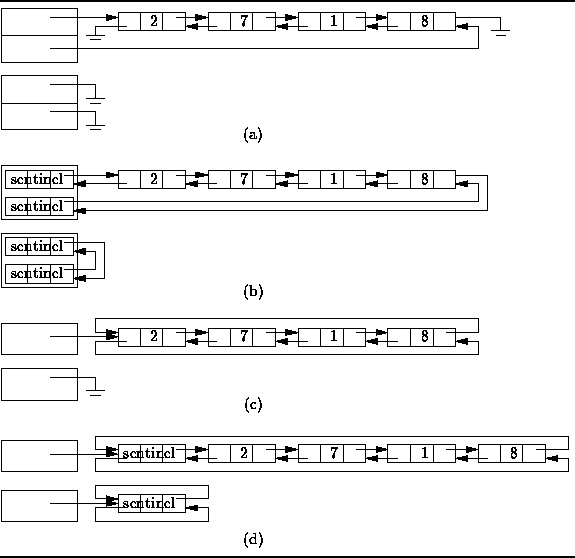
Figure: Doubly-Linked and Circular List Variations
Figure ![]() (a) shows the simplest case:
Two pointers, say head and tail,
are used to keep track of the list elements.
One of them points to the first element of the list,
the other points to the last.
The first element of the list has no predecessor,
therefore that pointer is null.
Similarly, the last element has no successor
and the corresponding pointer is also null.
In effect, we have two overlapping singly-linked lists
which go in opposite directions.
Figure
(a) shows the simplest case:
Two pointers, say head and tail,
are used to keep track of the list elements.
One of them points to the first element of the list,
the other points to the last.
The first element of the list has no predecessor,
therefore that pointer is null.
Similarly, the last element has no successor
and the corresponding pointer is also null.
In effect, we have two overlapping singly-linked lists
which go in opposite directions.
Figure ![]() also shows the representation of an empty list.
In this case the head and tail pointers are both null.
also shows the representation of an empty list.
In this case the head and tail pointers are both null.
Figure ![]() (b) shows a case which uses sentinels.
In this variation two sentinels are used!
Because there are in effect two overlapping linked lists
that go in opposite directions,
two sentinels are used--one for each singly-linked list.
Recall, the use of a sentinel is motivated by the fact that
the code for insertion and deletion is often simpler to write
because there are fewer special cases to consider.
Figure
(b) shows a case which uses sentinels.
In this variation two sentinels are used!
Because there are in effect two overlapping linked lists
that go in opposite directions,
two sentinels are used--one for each singly-linked list.
Recall, the use of a sentinel is motivated by the fact that
the code for insertion and deletion is often simpler to write
because there are fewer special cases to consider.
Figure ![]() (b) shows that in the empty list,
the two sentinels point to each other.
(b) shows that in the empty list,
the two sentinels point to each other.
A circular, doubly-linked list is shown in
Figure ![]() (c).
A circular list is formed by making
use of pointers which would otherwise be null:
The last element of the list is made the predecessor of the first element;
the first element, the successor of the last.
The upshot is that we no longer need both a head and tail pointer to
keep track of the list.
Even if only a single pointer is used,
both the first and the last list elements can be found in constant time.
(c).
A circular list is formed by making
use of pointers which would otherwise be null:
The last element of the list is made the predecessor of the first element;
the first element, the successor of the last.
The upshot is that we no longer need both a head and tail pointer to
keep track of the list.
Even if only a single pointer is used,
both the first and the last list elements can be found in constant time.
Finally, Figure ![]() (d) shows a circular,
doubly-linked list which has a single sentinel.
This variation is similar to the preceding one in that
both the first and the last list elements can be found in constant time.
This variation has the advantage that no special cases are
required when dealing with an empty list.
Figure
(d) shows a circular,
doubly-linked list which has a single sentinel.
This variation is similar to the preceding one in that
both the first and the last list elements can be found in constant time.
This variation has the advantage that no special cases are
required when dealing with an empty list.
Figure ![]() shows that the empty list is represented by a list
with exactly one element--the sentinel.
In the case of the empty list,
the sentinel is both is own successor and predecessor.
Since the sentinel is always present,
and since it always has both a successor and a predecessor,
the code for adding elements to the empty list
is identical to that for adding elements to a non-empty list.
shows that the empty list is represented by a list
with exactly one element--the sentinel.
In the case of the empty list,
the sentinel is both is own successor and predecessor.
Since the sentinel is always present,
and since it always has both a successor and a predecessor,
the code for adding elements to the empty list
is identical to that for adding elements to a non-empty list.