Binary Trees

This section presents an implementation of binary trees in the sense of Definition . A binary tree is essentially a N-ary tree where N=2. Therefore, it is possible to implemented binary trees using the NaryTree class presented in the preceding section. However, because the NaryTree class implementation is a general implementation which can accommodate any value of N, it is somewhat less efficient in both time and space than an implementation which is designed specifically for the case N=2. Since binary trees occur quite frequently in practice, it is important to have a good implementation.

Another consequence of restricting N to two is that we can talk of the left and right subtrees of a tree. Consequently the interface provided by a binary tree class is quite different from the general interface provided by an N-ary tree class.

Figure  shows how the binary tree given in Figure  is be represented. The basic idea is that each node of the tree contains two pointers to the subtrees of that node. Just as we did for N-ary trees, we represent explicitly the empty trees. Since an empty tree node contains neither root nor subtrees it is represented by a structure in which all the pointers have the value zero.

  
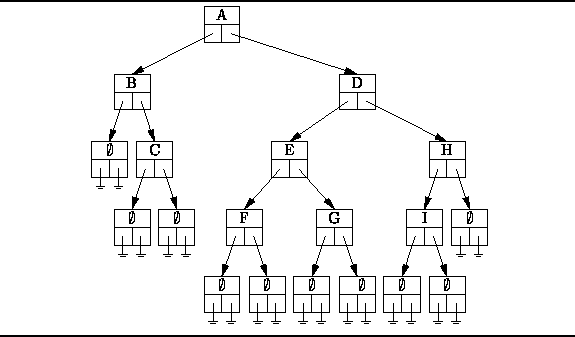
Figure: Representing Binary Trees

The BinaryTree class is declared in Program . It is derived from the same base class, Tree, as the classes GeneralTree and NaryTree. Therefore, it shares with those classes the common aspects of the tree and container interfaces. While the declarations of the three classes differ in the details, they all three follow a similar design pattern. Comparing Programs , and , we see that in addition to the constructors and destructor, they all possess similar routines for accessing and manipulating the root and the subtrees of a tree.

  
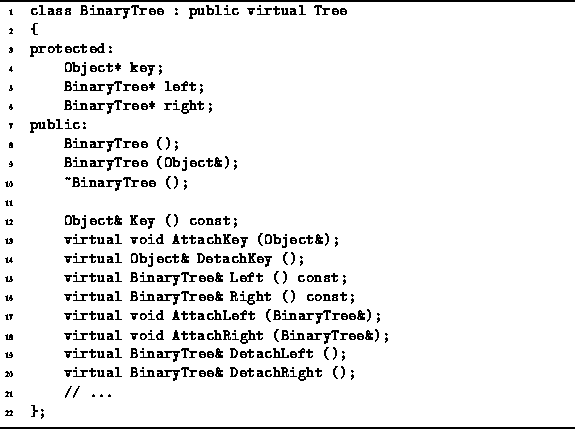
Program: BinaryTree Class Definition

• Member Variables
• Constructors
• Destructor and Purge Member Functions

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.