 Data Structures and Algorithms
with Object-Oriented Design Patterns in C++
Data Structures and Algorithms
with Object-Oriented Design Patterns in C++

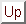



Definition (M-way Search Tree)
An M-way search tree
T is a finite set of keys.
Either the set is empty, 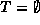 ; or
the set consists of n M-way subtrees
; or
the set consists of n M-way subtrees 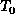 ,
, 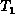 , ...,
, ..., 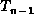 ,
and n-1 keys,
,
and n-1 keys, 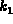 ,
, 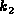 , ...,
, ..., 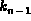 ,
,
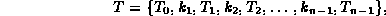
where 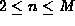 , such that the keys and nodes satisfy
the following data ordering properties :
, such that the keys and nodes satisfy
the following data ordering properties :
- The keys in each node are distinct and ordered,
i.e.,
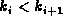 for
for 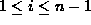 .
. - All the keys contained in subtree
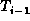 are less than
are less than 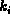 ,
i.e.,
,
i.e., 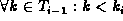 for
for 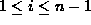 .
The tree
.
The tree 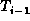 is called the left subtree
with respect to the key
is called the left subtree
with respect to the key 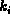 .
. - All the keys contained in subtree
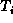 are greater than
are greater than 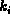 ,
i.e.,
,
i.e., 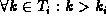 for
for 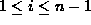 .
The tree
.
The tree 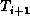 is called the right subtree
with respect to the key
is called the right subtree
with respect to the key 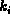 .
.
Figure  gives an example of an M-way search tree for M=4.
In this case,
each of the non-empty nodes of the tree has between one and three keys
and at most four subtrees.
All the keys in the tree satisfy the data ordering properties.
Specifically, the keys in each node are ordered
and for each key in the tree,
all the keys in the left subtree with respect to the given key are
are less than the given key,
and all the keys in the right subtree with respect to the given key
are larger than than the given key.
Finally, it is important to note that the topology of the tree
is not determined by the particular set of keys it contains.
gives an example of an M-way search tree for M=4.
In this case,
each of the non-empty nodes of the tree has between one and three keys
and at most four subtrees.
All the keys in the tree satisfy the data ordering properties.
Specifically, the keys in each node are ordered
and for each key in the tree,
all the keys in the left subtree with respect to the given key are
are less than the given key,
and all the keys in the right subtree with respect to the given key
are larger than than the given key.
Finally, it is important to note that the topology of the tree
is not determined by the particular set of keys it contains.
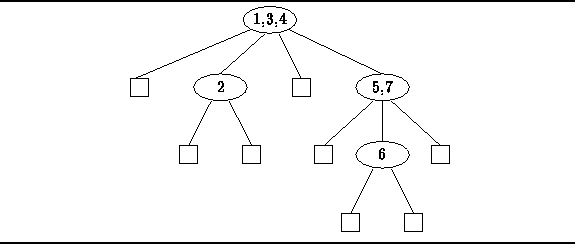
Figure: An M-way Search Tree




 Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.
Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.
![]()
![]() , such that the keys and nodes satisfy
the following data ordering properties :
, such that the keys and nodes satisfy
the following data ordering properties :
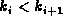 for
for 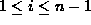 .
.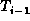 are less than
are less than 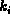 ,
i.e.,
,
i.e., 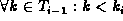 for
for 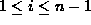 .
The tree
.
The tree 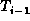 is called the left subtree
with respect to the key
is called the left subtree
with respect to the key 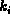 .
.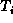 are greater than
are greater than 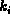 ,
i.e.,
,
i.e., 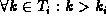 for
for 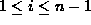 .
The tree
.
The tree 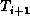 is called the right subtree
with respect to the key
is called the right subtree
with respect to the key  .
.
