Single Rotations

Data Structures and Algorithms with Object-Oriented Design Patterns in C++

Single Rotations

Figure (a) shows an AVL balanced tree. E.g., the balance factor for node A is zero, since its left and right subtrees have the same height; and the balance factor of node B is +1, since its left subtree has height h+1 and its right subtree has height h.

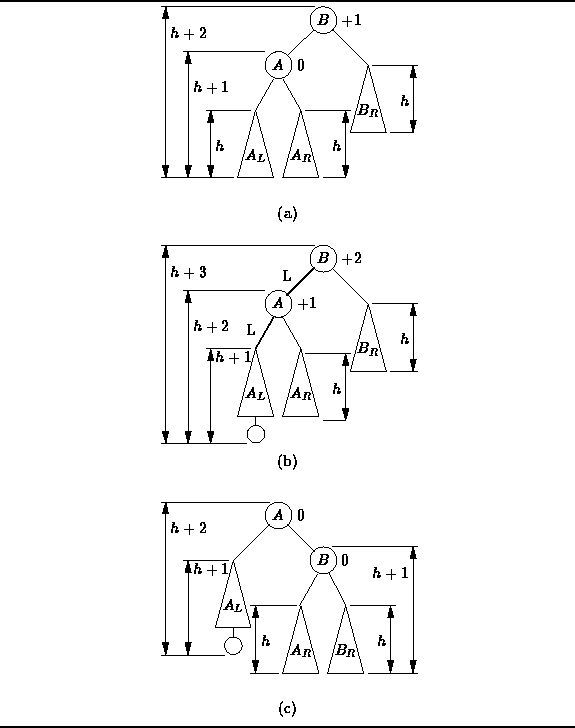
Figure: Balancing an AVL Tree with a Single (LL) Rotation

Suppose we insert an item into , the left subtree of A. The height of can either increase or remain the same. In this case we assume that it increases. Then, as shown in Figure (b), the resulting tree is no longer AVL balanced. Notice where the imbalance has been manifested--node A is balanced but node B is not.

Balance can be restored by reorganizing the two nodes A and B, and the three subtrees, , , and , as shown in Figure (c). This is called an LL rotation , because the first two edges in the insertion path from node B both go to the left.

There are three important properties of the LL rotation:

The rotation does not destroy the data ordering property so the result is still a valid search tree. Subtree remains to the left of node A, subtree remains between nodes A and B, and subtree remains to the right of node B.
After the rotation both A and B are AVL balanced. Both nodes A and B end up with zero balance factors.
After the rotation, the tree has the same height it had originally. Inserting the item did not increase the overall height of the tree!

Notice, the LL rotation was called for because the root became unbalanced with a positive balance factor (i.e., its left subtree was too high) and the left subtree of the root also had a positive balance factor.

Not surprisingly, the left-right mirror image of the LL rotation is called an RR rotation . An RR rotation is called for when the root becomes unbalanced with a negative balance factor (i.e., its right subtree is too high) and the right subtree of the root also has a negative balance factor.