Data Structures and Algorithms with Object-Oriented Design Patterns in C++

Sets, Multisets and Partitions

In mathematics a set is a collection of elements, especially a collection having some feature or features in common. The set may have a finite number of elements, e.g., the set of prime numbers less than 100; or it may have an infinite number of elements, e.g., the set of right triangles. The elements of a set may be anything at all--from simple integers to arbitrarily complex objects. However, all the elements of a set are distinct--a set may contain only one instance of a given element.

For example, , , and are all sets the elements of which are drawn from . The set of all possible elements, U, is called the universal set . Note also that the elements comprising a given set are not ordered. Thus, and are the same set.

There are many possible operations on sets. In this chapter we consider the most common operations for combining sets--union, intersection, difference:

union: The union (or conjunction ) of sets S and T, written , is the set comprised of all the elements of S together with all the element of T. Since a set cannot contain duplicates, if the same item is an element of both S and T, only one instance of that item appears in . If and , then .
intersection: The intersection (or disjunction ) of sets S and T is written . The elements of are those items which are elements of both S and T. If and , then .
difference: The difference (or subtraction ) of sets S and T, written S-T, contains those elements of S which are not also elements of T. I.e., the result S-T is obtained by taking the set S and removing from it those elements which are also found in T. If and , then .

Figure illustrates the basic set operations using a Venn diagram . A Venn diagram represents the membership of sets by regions of the plane. In Figure the two sets S and T divide the plane into the four regions labeled I-IV. The following table illustrates the basic set operations by enumerating the regions that comprise each set.

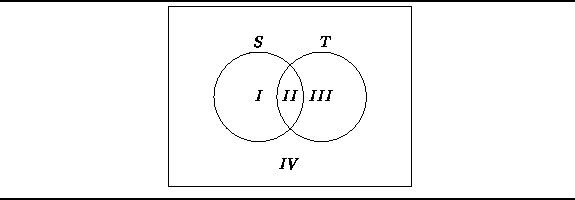
Figure: Venn Diagram Illustrating the Basic Set Operations

set region(s) of Figure

U I, II, III, IV

S I, II

S' III, IV

T II, III

I, II, III

II

S-T I

T-S III

set	region(s) of Figure
U	I, II, III, IV
S	I, II
S'	III, IV
T	II, III
	I, II, III
	II
S-T	I
T-S	III