Data Structures and Algorithms
with Object-Oriented Design Patterns in C++ 
Suppose we are given a sequence of n=5 words,
having lengths
, respectively,
which are to be typeset in a paragraph of width D=60.
Assume that the normal width of an inter-word space is s=10.
We begin by computing the lengths of all the subsequences of W
using Equation 
.
The lengths of all n(n-1)/2 subsequences of W
are tabulated in Table .
 | ||||||
|
i |  | j=1 | 2 | 3 | 4 | 5 |
| 1 | 10 | 10 | 20 | 30 | 42 | 92 |
| 2 | 10 | 10 | 20 | 32 | 82 | |
| 3 | 10 | 10 | 22 | 72 | ||
| 4 | 12 | 12 | 62 | |||
| 5 | 50 | 50 | ||||
Given , D and s,
it is a simple matter to apply 
to obtain the one-line penalties, 
,
which measure the amount of stretching or compressing needed
to set all the words in a given subsequence on a single line.
These are tabulated in Table .
| |  | |||||||||
|
i | j=1 | 2 | 3 | 4 | 5 | j=1 | 2 | 3 | 4 | 5 |
| 1 | 50 | 30 | 10 | 12 |  | 50 | 30 | 10 | 12 | 22 |
| 2 | 50 | 30 | 8 | | 50 | 30 | 8 | 18 | ||
| 3 | 50 | 28 | | 50 | 28 | 38 | ||||
| 4 | 48 | | 48 | 58 | ||||||
| 5 | 10 | 10 | ||||||||
Given the one-line penalties ,
we can use Equation to find for each subsequence of W
the minimum total penalty, ,
associated forming a paragraph from the words in that subsequence.
These are tabulated in Table .
The 
entry in Table gives the minimum total
cost of typesetting the entire paragraph.
The value 22 was obtained as follows:
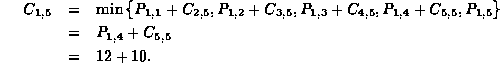
This indicates that the optimal solution is to set words
, 
, 
and 
on the first line of the paragraph
and leave 
by itself on the last line of the paragraph.
Figure illustrates this result.
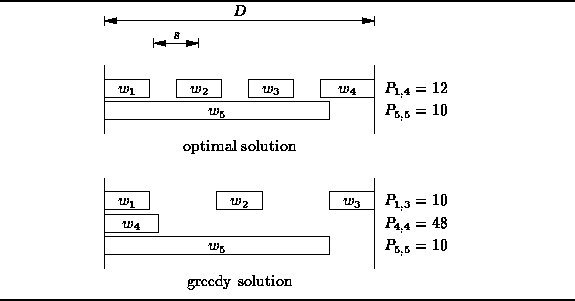
Figure: Typesetting a Paragraph
This formulation of the typesetting problem seems like overkill. Why not just typeset the lines of text one-by-one, minimizing the penalty for each line as we go? In other words why don't we just use a greedy strategy? Unfortunately, the obvious greedy solution strategy does not work!
For example,
the greedy strategy begins by setting the first line of text.
To do so it must decide how many words to put on that line.
The obvious thing to do is to select the value of k
for which 
is the smallest.
From Table
we see that 
has the smallest penalty.
Therefore, the greedy approach puts three words on the first line
as shown in Figure .
Since the remaining two words do not both fit on a single line,
they are set on separate lines.
The total of the penalties for the paragraph typeset using the greedy
algorithm is 
.
Clearly, the solution is not optimal
(nor is it very pleasing esthetically).
Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.